class: center, middle, inverse, title-slide # Algoritmos de Árboles y Colectividades ## Curso de aprendizaje automático para el INE ### Víctor Gallego y Roi Naveiro ### 2019-04-22 --- class: middle, center, inverse # Árboles de Clasificación y Regresión (CART) --- ## Introducción * Idea de los árboles: particionar el espacio de variables predictores en rectángulos. * Ajustar modelo muy sencillo a cada partición. * Tarea: encontrar usando el train las estructura del árbol (variables del corte y umbral) y el modelo en cada partición. -- * Punto fuerte: interpretabilidad * Importante en ciencias médicas: imita la forma de pensar de los doctores. 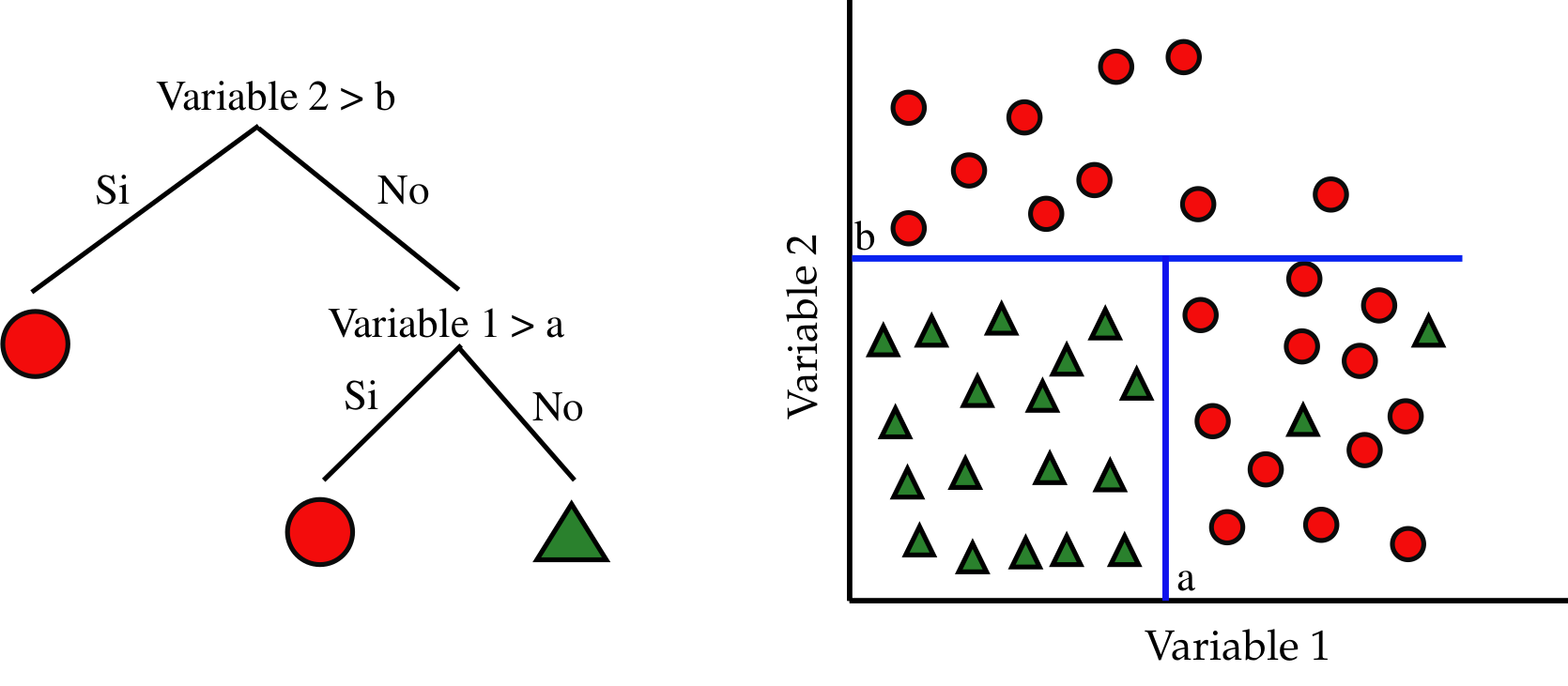 --- ## Árboles de regresión (1) * Sean datos de entrenamiento `\(\lbrace (x_i, y_i) \rbrace_{i=1}^N\)`, donde cada `\(x_i\)` es un vector de `\(p\)` variables predictoras. * Supongamos que particionamos el espacio de variables predictoras en `\(M\)` regiones `\(R_1, \dots, R_M\)` y para cada una ajustamos una constante `\(c_m\)`. La respuestas es `\begin{equation} f(x) = \sum_{m=1}^M c_m I(x \in R_m) \end{equation}` * Si nuestro criterio es minimizar `\(\sum (y_i - f(x_i))^2\)`, entonces dada la región `\(R_m\)` la mejor `\(c_m\)` es la media de los `\(y_i\)` de los `\(x_i \in R_m\)`. --- ## Árboles de regresión (2) * Buscar la mejor partición `\(R_1,\dots, R_M\)` en términos minimizar la suma de cuadrados es **computacionalmente inviable**. * Alternativa greedy: buscar mejores particiones binarias de forma secuencial. * Empezando con todos los datos, sea `\(j\)` la variable de partición y `\(s\)` el umbral. Esto define dos regiones del espacio `\(R_1\)` `\((X_j \leq s)\)` y `\(R_2\)` `\((X_j > s)\)`. * Hay que resolver `\begin{equation} \min_{j,s} \left[ \min_{c_1} \sum_{x_i \in R_1(j,s)} (y_i - c_1)^2 + \min_{c_2} \sum_{x_i \in R_2(j,s)} (y_i - c_2)^2\right] \end{equation}` -- * Para cada `\(j,s\)` el problema interno se resuelve inmediatamente: `\(c_1\)` es la media de los `\(y_i\)` de los `\(x_i \in R_1\)` (igual para `\(c_2\)`). * Para cada variable `\(j\)` encontrar el punto de partición `\(s\)` es rápido. * Se puede inspeccionar todas las variables de partición y encontrar el mejor par `\((j,s)\)`. * Iterar el proceso en las regiones resultantes. --- ## Árboles de regresión (3) * ¿Cuándo parar? * Árbol profundo hace overfitting, árbol pequeño tiene mucho sesgo. * Tamaño del árbol es un hiperparámetro. -- * Estrategia óptima: construír un árbol muy profundo `\((T_0)\)` y **podarlo**. * Sea `\(T\)` cualquier subárbol de `\(T_0\)` obtenido colapsando algún nodo interno. * Sea `\(|T|\)` el número de nodos terminales en `\(T\)` y `\(N_m\)` el número de instancias en el nodo terminal `\(m\)`-ésimo. Entonces `\begin{equation} Q_m(T) = \frac{1}{N_m} \sum_{x_i \in R_m} (y_i - \hat{c}_m)^2 \end{equation}` -- * El criterio a optimizar en la poda es `\begin{equation} \sum_{m=1}^{|T|} N_m Q_m(T) + \alpha |T| \end{equation}` --- ## Árboles de regresión (4) * El criterio a optimizar en la poda es `\begin{equation} C_\alpha (T) = \sum_{m=1}^{|T|} N_m Q_m(T) + \alpha |T| \end{equation}` * `\(\alpha\)` es un hiperparámetro que penaliza el tamaño de los árboles. * Para cada `\(\alpha\)` existe un subarbol `\(T_\alpha\)` tal que `\(C_\alpha (T_\alpha)\)` es mínimo. -- * Estrategia de búsqueda de `\(T_\alpha\)`: colapsar el nodo que produce el menos incremento en `\(\sum_{m=1}^{|T|} N_m Q_m(T)\)`, hasta quedarnos con un solo nodo. * Esta secuencia de subárboles contiene el óptimo! --- ## Árboles de clasificación * Debemos cambiar el criterio para particionar y para podar. * Sea un nodo `\(m\)` que representa la región `\(R_m\)` con `\(N_m\)` observaciones. Definimos `\(\hat{p}_{mk}\)` como la proporción de instancias de clase `\(k\)` en el nodo `\(m\)`. * Denominamos `\(k(m)\)` a la clase mayoritaria en el nodo `\(m\)` (aquella para la cual `\(\hat{p}_{mk}\)` es máximo) -- * **Medidas de impuridad** 1. Error de clasificación: `\(1 - \hat{p}_{mk(m)}\)` 2. Índice de Gini: `\(\sum_{k=1}^K \hat{p}_{mk} (1- \hat{p}_{mk})\)` 3. Entropía cruzada: `\(- \sum_{k=1}^K \hat{p}_{mk} \log \hat{p}_{mk}\)` * Gini y entropía cruzada **son diferenciables**. * OJO: pesar con número de ejemplos en cada partición resultante!! Es decir, minimizar `\begin{equation} n_L Q_L + n_R Q_R \end{equation}` --- ## Detalle técnico (1) * **Ejercicio**: ¿Cuántas particiones posibles de una variable categórica con `\(q\)` categorías en dos grupos existen? -- * Fácil ver que `\(2^{q-1} - 1\)`. **Escalado catastrófico**. * Si la respuestas es binaria (0-1) hay solución. Sea `\(x\)` variable categórica con categorías `\(x^1, \dots, x^q\)`. * Ordenamos las categorías en orden creciente de `\(P(Y=1|x=x_i)\)`. * El corte óptimo es alguno de los que respeta este orden, si la impureza es Gini o entropía cruzada. -- * También se cumple para output cuantitativo ordenando en valor creciente de la media de la respuesta. --- ## Detalle técnico (2)  --- class: middle, center, inverse # Boosting --- ## Aprendiendo de los errores * Dado un dataset de entrenamiento `\(\lbrace (x_i, y_i) \rbrace_{i=1}^N\)`, ajustamos un modelo `\(G(x)\)` y calculamos la tasa de error sobre el conjunto de entrenamiento `\begin{equation*} err = \frac{1}{N} \sum_{i=1}^N I(y_i \neq G(x_i)) \end{equation*}` * Partiendo de que `\(G(x)\)` es un clasificador débil, ¿cómo podemos hacer que además vaya corrigiendo sus errores? -- * **Boosting**: iremos aplicando el algoritmo a versiones modificadas de los datos de entrenamiento, obteniendo una secuencia de clasificadores `\begin{equation*} G_m(x),\quad m=1,\ldots,M \end{equation*}` --- ## Aprendiendo de los errores <center>  </center> --- ## AdaBoost.M1 (1997) (1) * **Idea**: remuestrear los datos de entrenamiento, dando mayor peso a las instancias mal clasificadas. * Algoritmo: input: `\((x_i, y_i),\qquad y_i \in \lbrace -1, +1 \rbrace,\qquad 1 \leq i \leq N\)`. 1. Inicialmente pesos uniformes: `\(w_i = \frac{1}{N}\)` 2. Desde `\(m=1\)` hasta `\(M\)`: + Ajustar `\(G_m(x)\)` a los datos de entrenamiento + Calculamos el error sobre la muestra de entrenamiento + Aumentamos `\(w_i\)` en los ejemplos mal clasificados --- ## AdaBoost.M1 (1997) (2) * Algoritmo: input: `\((x_i, y_i),\qquad y_i \in \lbrace -1, +1 \rbrace,\qquad 1 \leq i \leq N\)`. 1. Inicialmente pesos uniformes: `\(w_i = \frac{1}{N}\)` 2. Desde `\(m=1\)` hasta `\(M\)`: + Ajustar `\(G_m(x)\)` a los datos de entrenamiento + Cálculo del error ponderado: `\begin{equation*} err_{m} = \frac{\sum_{i=1}^N w_i I(y_i \neq G_m(x_i))}{\sum_{i=1}^N w_i} \end{equation*}` + Calcular `\begin{equation*} \alpha_m = \log(\frac{1-err_m}{err_m}) \end{equation*}` + Actualizar los pesos `\begin{equation*} w_i \leftarrow w_i \exp \lbrace \alpha_m I(y_i \neq G_m(x_i)) \rbrace \end{equation*}` 3. Predecir con `\(G(x) = \mbox{sign} \left[ \sum_{m=1}^M \alpha_m G_m(x) \right]\)` --- ## ¿Qué ajusta realmente boosting? * Ajusta un modelo aditivo (GAM) de la forma `\begin{equation*} f(x) = \sum_{m=1}^M \beta_m b(x; \gamma_m) \end{equation*}` * En el ámbito de los GAMs los parámetros `\(\beta_m, \gamma_m\)` se ajustan de forma conjunta. * En boosting, esos parámetros se ajustan por etapas (en cada `\(m\)`), lo que conduce a un **aprendizaje lento** pero que en la práctica **reduce el sobreajuste** (overfitting). --- ## Mínimos cuadrados por etapas (stagewise LS) 1. Tenemos `\begin{equation*} f_{m-1}(x) = \sum_{j=1}^{m-1} \beta_j b(x; \gamma_j) \end{equation*}` 2. Resolvemos `\begin{equation*} \min_{\beta, \gamma} \sum_{j=1}^N (y_i - f_{m-1}(x_i) - \beta b(x_i; \gamma))^2 \end{equation*}` * Esto es: añadimos el término `\(\beta_m b(x; \gamma_m)\)` que mejor ajuste los **residuales** ( `\(y_i - f_{m-1}(x_i)\)` ) tras la iteración `\(m-1\)`. -- * Podemos **generalizarlo cambiando la función de coste cuadrático**. --- ## La función de coste exponencial * Introducimos esta nueva función de coste: `\begin{equation*} L(y, f(x)) = \exp (-y f(x)) \end{equation*}` * En cada iteración, hay que resolver `\begin{equation*} \min_{\beta, \gamma} \sum_{j=1}^N \exp(- y_i f_{m-1}(x_i) + \beta b(x_i; \gamma)) \end{equation*}` -- * ¿Por qué el coste exponencial? * Es una cota superior monótona y diferenciable del error de clasificación. * Da lugar a una actualización de remuestreo simple. * `\(\mbox{argmin}_{f(x)} \mathbb{E}_{Y|x} \left[ \exp(-Yf(x))\right] = \frac{1}{2} \log \frac{P(Y = +1|x)}{P(Y = -1|x)} \rightarrow P(Y = +1|x) = \frac{1}{1 + \exp(-2 f^*(x))}\)`, lo cual justifica la regla predictiva del signo. <center>  </center> --- ## Otras funciones objetivo * Clasificación + Exponencial: `\(\exp(-yf(x))\)`. + Desviación binomial (más robusta): `\(\log (1 + \exp(-2yf(x)))\)`. -- * Regresión + Cuadrático: `\(\frac{1}{2}(y - f(x))^2\)`. + Valor absoluto: `\(| y - f(x) |\)`. --- ## Implementación con árboles * ¿Qué usamos como modelo débil dentro del esquema de boosting? * Hastie, Tibshirani et al. argumentan que los árboles de decisión son excelentes para ser usados como clasificadores/regresores débiles (ver siguiente slide) -- * Por tanto, la estructura del modelo colectivo será `\begin{align*} f_M(x) = \sum_{m=1}^M T(x, \Theta_m) \end{align*}` * donde `\(T(x, \Theta) = \sum_{j=1}^J c_j I(x \in R_j)\)` es un árbol de decisión. --- ## Implementación con árboles <center>  </center> --- ## Gradient Boosting * En cada iteración, habrá que resolver `\begin{equation*} \hat{\Theta}_m = \mbox{argmin}_{\Theta_m} \sum_{i=1}^N L(y_i, f_{m-1}(x_i) + T(x_i; \Theta_m)) \end{equation*}` * Resolverlo de forma exacta es muy costoso. -- * Aprovechando que la función de coste es diferenciable, calculamos los gradientes `\begin{equation*} g_{im} = \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f(x_i) = f_{m-1}(x_i)} \end{equation*}` * `\(f_{m-1}(x_i) - lr*g_{im}\)` tiene menos pérdida que `\(f_{m-1}(x_i)\)`. * Por tanto, `\(T(x_i, \Theta_m)\)` será un **árbol de regresión** ajustado a predecir los gradientes `\(g_{im}\)` !! --- ## Gradient Boosting (Algoritmo) * Modelo inicial: `\(f_0(x) = \mbox{argmin}_{\gamma} \sum_{i=1}^N L(y_i, \gamma)\)` * Desde `\(m=1\)` hasta `\(M\)`: 1. Calcular gradientes `\(g_{im}\)`. 2. Ajustar un árbol de regresión al target `\(-g_{im}\)`, obteniendo las regiones terminales `\(R_{jm},j=1,\ldots,J_m\)`. 3. Para cada región `\(R_{jm}\)`, calcular `\(\gamma_{jm} = \mbox{argmin}_{\gamma} \sum_{x_i \in R_{jm}} L(y_i, f_{m-1}(x_i) + \gamma)\)`. 4. Actualizar: `\(f_{m} (x) = f_{m-1}(x) + \sum_{j=1}^{J_{m}} \gamma_{jm} I(x \in R_{jm})\)`. --- ## Hiperparámetros * `\(J_m\)`, tamaño de cada árbol: se tiende a escoger `\(J = J_m\)` para simplificar complejidad. * `\(J = 2\)`: no interacciones (solo hay una decisión/subdivisión). * `\(J = 3\)`: interacciones entre dos variables (subdivisiones sucesivas). * Con `\(J\)` se permiten hasta `\(J-1\)` interacciones. * Según ESL, típicamente escoger `\(4 \leq J \leq 8\)`. -- * `\(M\)`, número de iteraciones/árboles. * El error de entrenamiento se podría reducir arbitrariamente con `\(M \rightarrow \infty\)`. * Ajustarlo mediante un conjunto de validación, y dejar de iterar cuando el error de validación no mejore tras unas pocas iteraciones (**early stopping**). --- ## Regularización * `\(\eta \in \left[ 0, 1\right]\)`, tasa de muestreo/subsampling: * En lugar de estimar el gradiente sobre todo el conjunto de entrenamiento, `\(\mathcal{O}(N)\)`, * lo hacemos con una muestra aleatoria uniforme, `\(\mathcal{O}(\eta N)\)` (como en SGD). * Típicamente `\(\eta \leq 1/2\)`. -- * `\(\nu \in \left[ 0, 1\right]\)`, parámetro de encogimiento/shrinkage: * Se sustituye `\(f_m(x) = f_{m-1}(x) + \sum_{j=1}^{J_m} \gamma_{jm} I (x \in R_{jm})\)` * por `\(f_m(x) = f_{m-1}(x) + \nu \sum_{j=1}^{J_m} \gamma_{jm} I (x \in R_{jm})\)`. * Controla la tasa de aprendizaje del boosting. * Empíricamente `\(\nu\)` bajo favorece generalización (bajo error en test), aunque hace que aumente el número de iteraciones `\(M\)`. --- ## Interpretabilidad ### Importancia de variables * Para un solo árbol, Breiman propuso como medida de **importancia de una variable** `\(X_l\)` `\begin{equation*} \mathcal{I}_l^2 (T) = \sum_{t=1}^{J-1} \hat{i}_t^2 I(v(t) = l), \end{equation*}` (En cada nodo `\(t\)`, una de las variables `\(X_{v(t)}\)` es la escogida para hacer el corte en dos subregiones. Tal variable escogida es la que maximiza la mejora estimada en el riesgo cuadrático `\(\hat{i}_t^2\)`) * Para un conjunto de `\(M\)` árboles, podemos promediarla `\begin{equation*} \mathcal{I}_l^2 = \frac{1}{M} \sum_{m=1}^{M} \mathcal{I}_l^2 (T). \end{equation*}` --- ## Interpretabilidad ### Gráficos de dependencia parcial * Dividimos las variables predictoras `\(X = (X_1, X_2, \ldots, X_p)\)` en dos grupos disjuntos: `\begin{equation*} X = (X_{\mathcal{S}}, X_{\mathcal{C}})\mbox{ tal que } \mathcal{S} \cup \mathcal{C} = \lbrace 1, 2, \ldots, p \rbrace. \end{equation*}` * En lugar de inspeccionar la respuesta (por ej, probabilidad de +) `\(f(X)\)`, representamos una aproximación definida sobre `\(X_{\mathcal{S}}\)`: `\begin{equation*} f_{\mathcal{S}} (X_{\mathcal{S}}) = \mathbb{E}_{X_{\mathcal{C}}} \left[ f(X_{\mathcal{S}}, X_{\mathcal{C}})\right] \approx \frac{1}{N} \sum_{i=1}^N f(X_{\mathcal{S}}, x_{i\mathcal{C}}) \end{equation*}` * `\(|\mathcal{S}|\)` bajo para poder visualizarlo. * Ejemplo en los ejercicios de hoy. --- ## Interpretabilidad * Gráfico de dependencia parcial para detección de spam: aumento del uso del símbolo ! aumenta probabilidad de spam, mientras que con la marca HP sucede a la inversa.  --- ## Librerías para R * **gbm**: la implementación original. Soporta gráficos de dependencia parcial para interpretabilidad. * https://cran.r-project.org/web/packages/gbm/index.html * **xgboost**: usada por varios ganadores de la plataforma Kaggle. ~10 veces más rápida que gbm, soporta matrices dispersas. También soporta boosting de modelos lineales. * https://cran.r-project.org/web/packages/xgboost/index.html --- ## Resumen * Boosting como proceso de **optimización por etapas y suave**. Por ejemplo, **gradient boosting** aproxima los gradientes en cada iteración por un árbol ajustado a ellos. * Boosting como alternativa al bagging. Mientras que boosting es un proceso que busca la **reducción del sesgo**, el bagging se emplea como **reducción de la varianza**. * Fácil de hacer overfiting: usar conjunto de validación como **terminación temprana**. * **Interpretabilidad decente**: importancia de variables y gráficos de dependencia parcial. --- class: middle, center, inverse # Random Forest --- ## Introducción - Bootstrap * Técnica para medir precisión de estimadores. * Permite estimar la distribución de casi cualquier estadístico (y por tanto cualquier propiedad de interés, como la varianza). -- * Idea 1. Muestrear al azar los datos de entrenamiento **con reemplazo**. 2. Generar `\(B\)` *muestras bootstrap*, del mismo tamaño que el train. 3. En cada muestra, calcular el estadístico de interés: **bootstrap estimates**. 4. La distribución empírica de las **bootstrap estimates** es una estimación de la distribución del estimador. --- ## Introducción - Bagging * Además de servir para cuantificar la predicción de una estimación, el bootstrap puede usarse para mejorar la predicción! * Ajustamos **modelo de regresión** a datos de entrenamiento `\(T = \lbrace (x_1,y_1), \dots, (x_N, y_N)\rbrace\)` * `\(\hat{f}(x)\)` es la predicción del modelo en el punto `\(x\)`. -- * **Bagging** (bootstrap aggregation) promedia esta predicción sobre una colección de muestras bootstrap del conjunto de entrenamiento, * Para cada muestra bootstrap `\(T^{i}\)`, `\(i = 1,2, \dots, B\)` ajustamos el modelo obteniendo `\(f^{i}(x).\)` La estimación de bagging es `\begin{equation} \hat{f}_{bag} = \frac{1}{B} \sum_{i=1}^B f^{i}(x) \end{equation}` * Interesante para árboles pues cada árbol bootstrap *se fijará* en variables diferentes. --- ## Introducción - Bagging * En **clasificación** cada muestra bagging predice una clase. La predicción final será la clase más votada. * Para estimar probabilidades no usar proporciones de votos. Promediar la estimaciones de probabilidad de cada muestra (por ejemplo en árboles de decisión la proporción de las clases en nodos terminales). -- * Bagging es una técnica para reducir la varianza de una función predictiva. * De forma empírica: funciona bien para procedimientos con poco sesgo y mucha varianza (árboles de decisión). --- ## Introducción - Random Forests * Random Forests es una modificación de bagging de árboles de decisión, que produce un comité de árboles **decorrelados**. * Resultados similares a boosting pero más sencillos de entrenar y tunear.  --- ## RF - Bagging * La idea subyacente es promediar muchos modelos ruidosos pero aproximadamente insegados y así reducir la varianza. * Los árboles son candidatos ideales: si son profundos son aproximadamente insesgados. * Como cada árbol generado con bagging está idénticamente distribuido, la media de `\(B\)` árboles de bagging es la misma. * El sesgo de los predicción del bagging de árboles es el mismo que el de cada árbol individual. Podemos mejora reduciendo varianza.., --- ## RF - Bagging * Intuición en regresión: si el training set `\((x_i, y_i)\)` con `\(i=1,2, \dots, N\)` es iid de la distribución `\(P\)`, el estimador agregado ideal es `\(f_{ag}(x) = \mathbb{E}_P(\hat{f}^*(x))\)` (aquí las muestras bootstrap son muestras de tamaño `\(N\)` de P). `\begin{eqnarray} \mathbb{E}_P [Y- \hat{f}^*(x)]^2 &=& \mathbb{E}_P [Y - f_{ag}(x) + f_{ag}(x) - \hat{f}^*(x)]^2 \\ &=& \mathbb{E}_P[Y - f_{ag}(x)]^2 + \mathbb{E}_P[f_{ag}(x) - \hat{f}^*(x)]^2 \\ &\geq& \mathbb{E}_P[Y - f_{ag}(x)]^2 \end{eqnarray}` -- * La agregación usando la población real **nunca** incrementa el error cuadrático medio. * Esto sugiere que usando baggin con los datos de train quizás disminuiremos el error cuadrático medio... --- ## RF - Decorrelación * La media de `\(B\)` variables aleatorias independientes e idénticamente distribuidas tiene varianza `\(\frac{1}{B} \sigma^2\)`. * (Ejercicio) Si las variables son simplemente idénticamente distribuidas (pero no independientes) con correlación positiva `\(\rho\)` entonces la varianza de la media es `\begin{equation} \rho \sigma^2 + \frac{1-\rho}{B}\sigma^2 \end{equation}` -- * Al aumentar `\(B\)` el segundo término se anula. * Podemos mejorar la reducción de la varianza si reducimos `\(\rho\)` (sin pasarse para no aumentar mucho `\(\sigma^2\)`). * En RF se consigue así: Antes de cada separación en cada árbol, seleccionar al azar `\(m\)` variables predictoras y buscar el corte óptimo usando solo esas. * Menor `\(m\)` `\(\Rightarrow\)` Menor `\(\rho\)`. --- ## Ejercicio Si las variables son simplemente idénticamente distribuidas (pero no independientes) con correlación positiva `\(\rho\)` entonces la varianza de la media es `\begin{equation} \rho \sigma^2 + \frac{1-\rho}{B}\sigma^2 \end{equation}` Tenemos que `\begin{eqnarray} \text{Var} \left( \frac{1}{B} \sum X_i \right) = \frac{1}{B^2} \text{Var} \left( \sum X_i \right) = \frac{1}{B^2} \left[ \mathbb{E} \left[\left(\sum X_i \right)^2 \right] - \mathbb{E} \left[\sum X_i\right]^2 \right] \end{eqnarray}` El segundo término vale `\begin{eqnarray} \mathbb{E} \left[\sum X_i\right]^2 = B^2 \mu^2 \end{eqnarray}` El primero `\begin{eqnarray} \mathbb{E} \left[\left(\sum X_i \right)^2 \right] = \mathbb{E} \left[ \left(\sum_{i=1}^B X_i^2 \right) + 2 \left(\sum_{i=1}^B \sum_{j<i} X_i X_j \right) \right] = B(\sigma^2 + \mu^2) + B(B-1)(\rho \sigma^2 + \mu^2) \end{eqnarray}` Sustituyendo llegamos a la expresión de partida. --- ## RF - Detalles Técnicos * En **regresión**: hacer la media de predicción de cada árbol. * En **clasificación**: voto mayoritario. -- * En **regresión** se recomienda: `\(m = p/3\)` y tamaño mínimo de nodos para permitir división 5. * En **clasificaión** se recomienda: `\(m = \sqrt{p}\)` y tamaño mínimo de nodos 1. * Mejor tunear estos hiperparámetros (son los más importantes). -- * RF es muy fácil de tunear y suele dar buenos resultados: recomendable usarlo como primera opción. * Además es trivial de paralelizar!! --- ## Muestras *Out of bag* * RF permite hacer validación cruzada al mismo tiempo que se entrena!! * En cada muestra bootstrap, es fácil probar que aproximadamente `\(1/3\)` de observaciones quedan fuera del correspondiente árbol. * Estas se denominan muestras *Out of Bag* (OOB). -- * Para construír una estimación del OOB: Para cada observación `\((x_i, y_i)\)` construír su predictor promediando únicamente los árboles correspondientes a muestras bootstrap donde no aparece `\((x_i, y_i)\)`. * Esta estimación es asintóticamente idéntica a la obtenida con N-fold cross validation. * Usar esto para validar los hiperparámetros de interés! -- * Se puede probar que RF no incremenetan el error de generalización cuando se añaden más árboles. * Luego se puede observar el comportamiento del error OOB y terminar el entrenamiento cuando este se estabiliza. --- ## Medidas de importancia de las variables * Dos formas posibles de medir importancia. * Para cada variable `\(m\)` medir cuánto decrece el criterio de impuridad Gini (o la entropía) en cada corte de esta variable y cada árbol del bosque. * Sumar a todos los árboles. -- * Pasar las muestras oob por el enésimo árbol y calcular la precisión. * Permutar aleatoriamente el valor de la variable `\(m\)` en las muestras OOB y calcular de nuevo la precisión. * Promediar el decrecimiento en precisión en todos los árboles del bosque. * Cuanto más decrece la precisión debido a permutaciones de la variable `\(m\)`, más importante es la variable- -- * La medida de decrecimiento del criterio de impuridad puede favorecer a variables con número de categorías muy alto (respecto a variables con pocas categorías). --- ## Matrices de proximidad y valores ausentes * Al crecer un RF, se puede calcular la metriz `\(N \times N\)` de proximidad. * Para cada árbol, cualquier par de observaciones OOB que compartan el nodo terminal, incrementar su proximidad en una unidad. -- * Esto puede utilizarse para imputar valores ausentes. * En primer lugar, rellenar los valores ausentes de manera poco precisa (mediana o moda de ejemplos de la misma clase). * Calcular la matriz de proximidad. -- * Para una variable contínua `\(m\)`, si es ausente en el ejemplo `\(n\)`, imputarla con la media de los valores no ausentes de esa variable, pesada con la proximidad entre el ejemplo `\(n\)` y el ejemplo no ausente. * Si es categórica, imputar con el valor más frecuente, con frecuencias pesadas con la proximidad. --- class: middle, center, inverse # Métodos basados en Colectividades --- * **Ensembling methods**, también denominados **comités** de modelos. * Supongamos que tenemos 3 clasificadores `\(G_i(x)\)`, que para cierta instancia `\(x_0\)` pronostican: `\begin{align*} G_1(x_0) &= 1 \\ G_2(x_0) &= 0 \\ G_3(x_0) &= 1 \\ \end{align*}` * ¿Qué clase deberíamos asignar a `\(x_0\)`? -- * Varias opciones: * **Voto uniforme**: cada modelo cuenta lo mismo * **Voto ponderado**: asignamos mayor peso a los modelos con más confianza. * **Regresión**: tomamos la media o la mediana. --- ## Ejemplo con dataset Iris * Árbol de clasificación (tasa de acierto: 92%) <center>  </center> --- ## Ejemplo con dataset Iris * kNN con `\(k=1\)` (tasa de acierto: 90.7%) <center>  </center> --- ## Ejemplo con dataset Iris * SVM (tasa de acierto: 92.7%) <center>  </center> --- ## Ejemplo con dataset Iris * Comité de los tres modelos anteriores, votación uniforme (tasa de acierto: **94%**) <center>  </center> --- ## ¿Por qué funciona esto? * Por ejemplo, asumimos que tenemos 10 observaciones a clasificar (0 ó 1), cuyas etiquetas reales son `\begin{align*} 1111111111 \end{align*}` -- * Tenemos tres modelos incorrelados entre sí, cada uno con un 70% de tasa de acierto. Por tanto, tres ejemplos de predicciones de cada modelo podrían ser `\begin{align*} 0110101111 \\ 1010111110 \\ 1101110011 \\ \end{align*}` -- * Al tomar la clase mayoritaria en cada observación, nos quedaría: `\begin{align*} 1110111111 \end{align*}` (90% de tasa de acierto) --- ## Ejercicio (1) * Para el caso de regresión, demostrar que si los errores de `\(M\)` modelos son incorrelados y de media `\(0\)`, entonces el error del comité es menor que los errores de cada modelo promediados -- * La predicción del comité viene dada por `\begin{equation*} y_{COM}(x) = \frac{1}{M} \sum_{m=1}^M y_m(x) \end{equation*}` * Supongamos que la verdadera función de regresión es `\(h(x)\)`, por lo que cada modelo es de la forma `\begin{equation*} y_m(x) = h(x) + \epsilon_m(x) \end{equation*}` * El error (cuadrático) promedio es: `\begin{equation*} \mathbb{E}_x \left[ (y_m(x) - h(x))^2\right] = \mathbb{E}_x \left[ \epsilon_m(x)^2 \right] \end{equation*}` * El error, además promediado sobre `\(M\)`, es: `\begin{equation*} E_{PR} = \frac{1}{M} \sum_{m=1}^M \mathbb{E}_x \left[ \epsilon_m(x)^2 \right] \end{equation*}` --- ## Ejercicio (2) * El error promedio para el comité es `\begin{equation*} E_{COM} = \mathbb{E}_x \left[ ( \frac{1}{M} \sum_{m=1}^M y_m(x) - h(x) )^2 \right] = \mathbb{E}_x \left[ (\frac{1}{M}\sum_{m=1}^M \epsilon_m(x))^2 \right] \end{equation*}` * Con la hipótesis del enunciado: `\begin{align*} \mathbb{E}_x \left[ \epsilon_m(x) \right] &= 0 \\ \mathbb{E}_x \left[ \epsilon_m(x) \epsilon_n(x) \right] &= 0 \qquad n \neq m \end{align*}` * Obtenemos que `\begin{align*} E_{COM} = \mathbb{E}_x \left[ \frac{1}{M} \frac{1}{M} \sum_{m=1}^M \epsilon_m(x)^2 \right] = \frac{1}{M} E_{PR} \end{align*}` * En general, los (errores de los) modelos **no serán totalmente incorrelados**. --- ## Promediado Bayesiano de modelos (BMA) * Los comités tiene una interpretación bastante natural en Estadística Bayesiana. * Asumimos que tenemos `\(k = 1, \ldots, K\)` modelos distintos * `\(p(k)\)` es la importancia de cada modelo. * `\(p(y|x,k)\)` es la probabilidad de que el modelo `\(k\)` clasifique `\(x\)` como de clase `\(y\)`. * Por la Ley de Probabilidad Total: `\begin{align*} p(y|x) = \sum_{k=1}^K p(y|x,k)p(k) \end{align*}` * La suma sobre `\(k\)` representa nuestra incertidumbre sobre cual de los `\(k\)` modelos es el que más se aproxima a la realidad. --- ## Generalizando * Previamente teníamos un comité de la forma `\begin{align*} p(y|x) = \sum_{k=1}^K p(y|x,k)\mathbf{p(k)} \end{align*}` * ¿Por qué `\(p(k)\)` debería ser homogénea (igual en todo el dominio `\(\mathcal{X}\)`)? -- * Llegamos a las **mixturas de expertos** `\begin{align*} p(y|x) = \sum_{k=1}^K p(y|x,k)\mathbf{p(k|x)} \end{align*}` * Diferentes componentes se especializan en modelar distintas regiones del espacio `\(\mathcal{X}\)`. * La visión probabilista/Bayesiana del aprendizaje automático permite este tipo de construcciones, y da algoritmos generales para ajustarlos (como el algoritmo EM). * Más en las sesiones de modelos Bayesianos / Aprendizaje profundo.