Visualización de datos

# Visualización de datos
## Explotación y visualización
### Alberto Torres Barrán
### 2020-02-29

---

## Introducción

* Visualizar datos es mitad ciencia mitad arte

* Una buena visualización:

1. representa los datos de forma correcta
  
  2. es estéticamente agradable, sin elementos que distraigan del mensaje principal que queremos transmitir
  
* Se han visto al menos dos herramientas para realizar gráficos: matplotlib y ggplot2

* En esta sesión:

1. como pasar de los datos al tipo de gráfico más adecuado

2. directorio con los tipos de gráficos más comunes (no todos!)
  
  3. conceptos independientes de la herramienta concreta

---

## Gramática de gráficos

* Descripción precisa de todos los componentes necesarios para realizar una visualización

* Wilkinson, L. (2005), *The Grammar of Graphics*

* Una de las implementaciones más conocidas es la librería `ggplot2`:

* Wickham, H. (2009), [*ggplot2: Elegant Graphics for Data Analysis*](https://ggplot2-book.org/)

* Artículo con las implicaciones de trasladar los conceptos de la gramática de gráficos a un lenguaje de programación (R):

* Wickham, H. (2010), [*A Layered Grammar of Graphics*](https://vita.had.co.nz/papers/layered-grammar.pdf)

---

## Fundamentos de visualización de datos

* Wilke, C. O., (2019) [Fundamentals of data visualization](https://serialmentor.com/dataviz/)

* Guía moderna para realizar visualizaciones que:

1. reflejan los datos de forma precisa
  
  2. cuentan una historia
  
  3. tienen una estética profesional
  
* Conceptos independientes de la herramienta que se usa!

* Los ejemplos del libro están hechos con `ggplot2` y otras librerías auxiliares

* Referencia principal de esta sesión (material en [Github](http://albertotb.com/curso-uam-dataviz/))

---

# Visualización de datos

---

## Características estéticas

* Toda visualización es una correspondencia entre datos y características estéticas

* Ejemplo: un gráfico de dispersión representa la relación entre dos variables, **x** e **y**, mediante puntos

* Dos tipos:

1. pueden representar datos continuos
  
  2. **no** pueden representar datos continuos
  
---

## Ejemplos

¿Cuáles de los siguientes elementos **no** pueden representar datos continuos?
![:vspace 4]

---

## Tipos de datos

* Independientes del lenguaje de programación/herramienta!

1. **Numéricos continuos**: números decimales
  
  2. **Numéricos discretos**: por ej. números enteros
  
  3. **Categóricos**: con o sin orden, por ej. las CC.AA de España
  
  4. **Fechas/horas**: pueden ser continuos o discretos dependiendo de lo que representen
  
  5. **Texto**

---

## Ejemplo

¿Qué tipos de datos hay en la siguiente tabla?

<table>
 <thead>
  <tr>
   <th style="text-align:left;"> Fecha y hora </th>
   <th style="text-align:right;"> Temperatura (ºC) </th>
   <th style="text-align:right;"> Viento (km/h) </th>
   <th style="text-align:left;"> Dirección del viento </th>
   <th style="text-align:left;"> Estacion </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> 27/02/2020 00:00 </td>
   <td style="text-align:right;"> 7.1 </td>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:left;"> Noroeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 01:00 </td>
   <td style="text-align:right;"> 6.3 </td>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 02:00 </td>
   <td style="text-align:right;"> 6.3 </td>
   <td style="text-align:right;"> 5 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 03:00 </td>
   <td style="text-align:right;"> 6.6 </td>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 04:00 </td>
   <td style="text-align:right;"> 5.9 </td>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 05:00 </td>
   <td style="text-align:right;"> 4.3 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Calma </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 06:00 </td>
   <td style="text-align:right;"> 4.2 </td>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:left;"> Sudoeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 07:00 </td>
   <td style="text-align:right;"> 4.6 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Calma </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 08:00 </td>
   <td style="text-align:right;"> 6.4 </td>
   <td style="text-align:right;"> 6 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 09:00 </td>
   <td style="text-align:right;"> 7.3 </td>
   <td style="text-align:right;"> 13 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 27/02/2020 10:00 </td>
   <td style="text-align:right;"> 9.4 </td>
   <td style="text-align:right;"> 11 </td>
   <td style="text-align:left;"> Oeste </td>
   <td style="text-align:left;"> El Goloso </td>
  </tr>
</tbody>
</table>

---

## Escalas

* Definen la equivalencia entre valores y elementos del gráfico

* Correspondencia 1 a 1 para evitar gráficos ambiguos

![:vspace 3]

---

## Ejemplo gráfico de líneas

## Ejemplo *heatmap*

![:vspace 8]

---

## Múltiples escalas

¿Cuántas escalas tiene el siguiente gráfico?

---

# Sistemas de coordenadas y ejes

---

## Sistemas de coordenadas

* Necesarios para cualquier tipo de visualización

* Determinan donde se van a posicionar los distintos valores

* Para gráficos estándar en 2D, necesitamos 2 valores para identificar una posición

* Además también necesitamos especificar la distribución relativa

* **Sistema de coordenadas**: combinación de escalas de posición y su distribución relativa

---

## Coordenadas cartesianas

* Sistema de coordenadas más habitual

* Dos ejes ortogonales con escalas continuas, **x** e **y**

* Invariantes frente a transformaciones lineales

---

## Ejemplo

---

## Ejes lineales vs no lineales

* **Eje lineal**: la separación entre dos líneas de la rejilla es la misma en la visualización que en las unidades de los datos

* **Eje no lineal**: la distancia entre dos líneas de la rejilla no es proporcional a la separación en las unidades de los datos

![:vspace 0.5]

---

## Escala logaritmica

* Escala no lineal más común

* Multiplicar en la escala logarítmica es como sumar en la escala lineal

* Conveniente para datos que provienen de multiplicaciones/divisiones, por ej. ratios

<table>
 <thead>
  <tr>
   <th style="text-align:right;"> poblacion </th>
   <th style="text-align:right;"> media </th>
   <th style="text-align:right;"> ratio </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 50 </td>
   <td style="text-align:right;"> 100 </td>
   <td style="text-align:right;"> 0.5 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 100 </td>
   <td style="text-align:right;"> 100 </td>
   <td style="text-align:right;"> 1.0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 200 </td>
   <td style="text-align:right;"> 100 </td>
   <td style="text-align:right;"> 2.0 </td>
  </tr>
</tbody>
</table>

![:vspace 3]

---

## Ejemplo

![](img/oceania-gdp-relative-1.png)

---

## Otras escalas

* Escala logarítmica es también útil cuando hay datos con magnitudes muy diferentes
  * Representar en una misma escala una ciudad con población 100 y otra con población 1M
  
* Problema: no puede haber 0 en la escala logarítimica (`log(0) = -inf`)

* En algunos casos pueden ser útiles otras transformaciones, por ej. la raíz cuadrada

---

## Ejemplo

![:vspace 7]

---

## Sistemas de coordenadas  curvos

* Las coordenadas polares son el ejemplo más común

* Especificamos una posición usando un ángulo y una distancia radial al origen

* Útiles para datos con periodicidad intrínseca

![:vspace 2]

---

## Ejemplo

---

## Datos geográficos

![](img/worldmap-four-projections-1.png)

---

## Otro ejemplo

Fuente: [ggradar](https://www.ggplot2-exts.org/ggradar.html)
]

---

## Otro (mal) ejemplo

Fuente: [Radar Plots usando ggplot2](https://rpubs.com/htejero/212368)
]

---

# Escalas de color

---

## Escalas de color cualitativas

* En variables categóricas, usamos el color para distinguir grupos que no tienen ningún orden

* Características deseables:

1. claramente **distinguibles** unos de otros
  
  2. **equivalentes**  
     * ningún color puede destacar sobre el resto
  
  3. distinguibles incluso para personas **daltónicas**

---

## Ejemplos

* Se pueden crear escalas personalizadas en la web [ColorBrewer 2.0](http://colorbrewer2.org/)

* También hay muchas disponibles:
    
  ![:scale 75%](img/qualitative-scales-1.png)

* A no ser que exista alguna razón de peso (por ej. colores corporativos), siempre es recomendable usar una de las múltiples escalas por defecto

* Muchas fueron creadas para cumplir las propiedades anteriores:
  
  * .footnotesize[Okabe, M., and K. Ito. (2008), [Color Universal Design (CUD): How to Make Figures and Presentations That Are Friendly to Colorblind People.](https://jfly.uni-koeln.de/color/)]

---

## Escalas de color secuenciales

* Con variables continuas, usamos escalas de color secuenciales

* Revelan patrones en nuestros datos que sería muy complicado ver de otra forma

* Simplifican a nuestro cerebro la tarea de procesar...
  
  * ...que valores son más pequeños que otros
  * ...distancia entre valores
  
* Características deseables [[A better default colormap for matplotlib](https://www.youtube.com/watch?v=xAoljeRJ3lU)]:

1. colorida
  2. agradable
  3. **secuencial**
  4. **perceptualmente uniforme**
  5. distinguible en **blanco y negro**
  6. accesible para personas **daltónicas**

* Una escala de color muy usada es [viridis](https://cran.r-project.org/web/packages/viridis/vignettes/intro-to-viridis.html)
---

## viridis

![](img/viridis.png)

---

## jet vs viridis

.center[.footnotesize[Fuente: [Hurricanes and Data Visualisation: Part I(b) – The Mona Lisa](https://peterjamesthomas.com/2017/09/15/hurricanes-and-data-visualisation-part-ib-the-mona-lisa/)]]

---

## Secuenciales vs divergentes

![:vspace 0.5]

---

## Ejemplo secuencial

---

## Ejemplo divergente

---

## Destacar elementos usando color

* Las escalas de color qualitativas se pueden modificar para resaltar ciertos grupos:

* creando versiones más oscuras y/o saturadas de algunos colores
  
  * combinando una escala de grises + color

* Importante que ninguno de los colores no-resaltados destaque sobre el resto!

* Otra opción es eliminar todo el color excepto el de los datos a resaltar

---

## Ejemplo resaltado

---

# Cantidades

---

## Cantidades

* Valores numéricos para un conjunto de categorías

* Énfasis: magnitud de los valores

* Tipos de gráfico:

1. gráfico de barras (*barplot*)
  
  2. gráfico de puntos (*dotplot*)
  
  3. mapas de calor (*heatmap*)
  
---

## Gráfico de barras

---

## Etiquetas rotadas

---

## Intercambiar ejes

---

## Orden de las categorias

---

## Variables cualitativas con orden

No usar orden alfabético ni orden creciente, sino el orden implícito de la variable

---

---

---

## Gráfico de barras agrupadas

¿Cómo ordenar las barras?

---

---

## Facetas

---

## Barras apiladas

* Útiles cuando las cantidades que representan por las barras apiladas es significativa

* Por ejemplo, número de personas

---

## Gráfico de puntos

En ocasiones podemos sustituir las barras por un únic punto

---

Si lo representáramos con barras, como el eje tiene que empezar en 0, el gráfico quedaría muy cargado

---

## Gráficos de barras: ejes

La cantidad de tinta debería de ser proporcional a la cantidad que se representa

---

En una escala lineal las barras siempre tienen que empezar en 0!!

---

## Mapas de calor (*heatmap*)

Enfatizan los patrones globales en lugar de los valores concretos

---

El orden es arbitrario

---

## Distribuciones

---

## Histogramas

* Representan la distribución de una variable numérica continua (quantitativa)

---

## Elección número de intervalos

* Siempre hay que probar con distintos tamaños de intervalo!

---

## Gráficos de densidad

* Estiman la densidad (distribución) de la variable usando una técnica conocidad como *Kernel Density Estimation* (KDE)

* Cuidado con el rango del eje x!

---

## Ancho del kernel

* Igual que en los historgramas la elección del ancho del kernel influye en los resultados

.footnotesize[
a) kernel Gaussiano, ancho = 0.5
b) kernel Gaussiano, ancho = 2
c) kernel Gaussiano, ancho = 5
d) kernel rectangular, ancho = 2
]

---

## Dos distribuciones

Los histogramas tienen problemas a la hora de mostrar múltiples distribuciones

---

## Transparencias

---

## Gráficos de densidad solapados

---

## Gráficos de densidad: facetas

---

## Histograma doble rotado

---

# Más de dos distribuciones

Si queremos representar las de dos los gráficos de densidad suelen ser preferibles a los histogramas

---

## Gráfico de cajas

Represente los principales estadísticos de una variable continua

---

---

Generalmente las barras verticales se usan para representar errores, no variabilidad en los datos (distribución)

---

## Gráficos "violín"

* Alternativa a los gráficos de cajas si hay un número de puntos suficientemente alto

* Se estima la densidad usando KDE, se rota 90 grados y se replica

![:scale 80%](img/violin-schematic-1.png)

---

Las desventajas son las mismas que los gráficos de densidad:
  
  * Pueden representar datos en zonas donde no los hay
  
  * Perdemos la noción de la cantidad de puntos

---

.footnotesize[Fuente: [Seaborn Library for Data Visualization in Python: Part 1](https://stackabuse.com/seaborn-library-for-data-visualization-in-python-part-1/)]
]

---

## *Strip chart*

Si no hay muchos puntos, podemos representarlos directamente

![:scale 90%](img/lincoln-temp-all-points-1.png)

---

## Ruido aleatorio

Generalmente es útil añadir un pequeño ruido aleatorio para que no se superpongan los puntos

![:scale 90%](img/lincoln-temp-jittered-1.png)

---

.footnotesize[Fuente: [Seaborn Library for Data Visualization in Python: Part 1](https://stackabuse.com/seaborn-library-for-data-visualization-in-python-part-1/)]
]

---

## *Ridgeline plot*

* Distribución de una variable continua para distintos grupos

* Similar al gráfico "violín", pero rotado

![:scale 85%](img/temp-ridgeline-1.png)

---

# Proporciones

---

## Gráficos circulares

.pull-left[
Ventajas:
 * Visualiza claramente las proporciones como parte de un conjunto
 * Visualiza fracciones como 1/2, 1/3,..

Desventajas:
 * Complicado comparar visualmente las proporciones relativas
]

---

## Gráficos de barras apilados

* Otra alternativa a los gráficos circulares
* Fracciones como 1/2, 1/3, etc. no son evidente de forma visual

---

## Gráficos de barras

Permiten visualizar de forma sencilla las proporciones relativas

---

## Otro ejemplo

Gráfico circular

* No se pueden distinguir las diferencias entre grupos

* No se pueden distinguir las diferencias entre años

---

Gráfico de barras apiladas

Excepto para los grupos A y E, no podemos compararlos visualmente

---

Gráfico de barras

---

Al igual que en los gráficos de barras que representan cantidades, el eje y tiene que empezar siempre en 0

.footnotesize[Fuente: [A Quick Guide to Spotting Graphics That Lie](https://www.nationalgeographic.com/news/2015/06/150619-data-points-five-ways-to-lie-with-charts/)]
]

---

## Gráficos de barras apilados (dos categorías)

Si solo hay dos categorías, no tenemos problema con los valores intermedios

---

## Gráficos de densidad apilados

* Si la variable es continua, podemos usar en su lugar un gráfico de densidad apilado

* No tenemos renferencia de los valores absolutos!

---

# Asociaciones de variables cuantitativas

---

## Gráfico de dispersión

Gráfico de puntos que representa 2 variables numéricas continuas

---

## Más de dos variables

Podemos representar una tercera variable (continua o discreta) usando el color con una escala apropiada

---

## Facetas

* Podemos usar también otros elementos estéticos del gráfico, como el tamaño de los puntos o su forma

* Si el gráfico está muy cargado, es conveniente separarlo en varios sub-gráficos (facetas)

---

## Gráfico de pares

Si tenemos más de dos variables cuantitativas, es común representar todos los pares posibles:

---

.footnotesize[Fuente: [seaborn.pairplot](https://seaborn.pydata.org/generated/seaborn.pairplot.html)]
]

---

## Correlogramas

* Para más de 3 o 4 variables, representar un gráfico de dispersión para cada uno de los pares posibles es complicado

* Una opción es resumir cada gráfico de dispersión calculando la correlación de las dos variables y representar ese valor

---

## Ejemplo

* Útil usar escala de color divergente

* Generalmente los límites son [-1, 1]

---

## Otro ejemplo

* Enfatizar correlaciones altas

---

## Reducción de dimensionalidad

---

# Series temporales y tendencias

---

## Una serie temporal

Podemos utilizar puntos, pero la diferencia es que el eje x representa tiempo y por tanto están ordenados

---

A menudo se combinan con lineas para enfatizar la dependencia temporal

---

* Si los datos tienen una frecuencia temporal alta, podemos eliminar los puntos

* Importante tener en cuenta que las líneas representan datos inventados!

---

**Solo** si el eje y empieza en 0, podemos colorear el area bajo la curva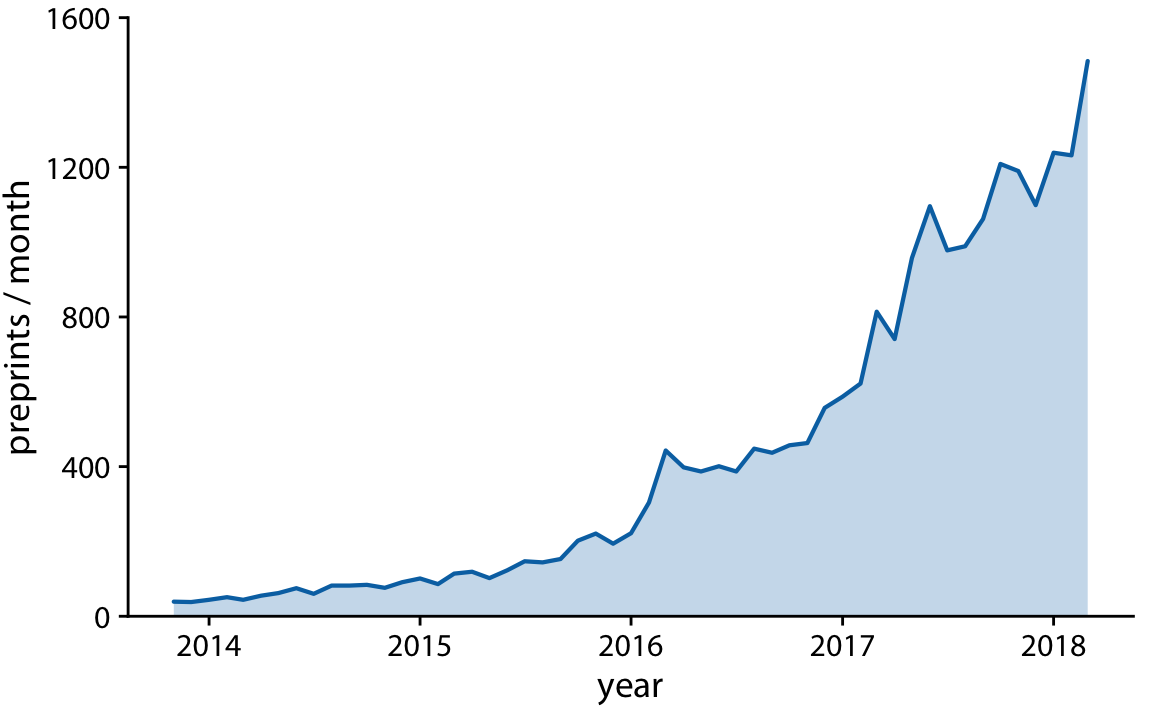

---

---

---

Hay que tener cuidado con las escalas!

.footnotesize[Fuente: [A Quick Guide to Spotting Graphics That Lie](https://www.nationalgeographic.com/news/2015/06/150619-data-points-five-ways-to-lie-with-charts/)]
]

---

## Multiples series temporales

---

---

* Siempre que sea posible, es conveniente etiquetar directamente el gráfico

* Sobre todo si hay un número elevado de categorías (8+)

---

## Gráficos de líneas

Útiles siempre que el eje x tenga un orden implícito, aunque no represente tiempo

---

## Múltiples series temporales con distintas unidades

---

Nunca usar dos escalas distintas en el mismo gráfico!

.footnotesize[Fuente: [A Quick Guide to Spotting Graphics That Lie](https://www.nationalgeographic.com/news/2015/06/150619-data-points-five-ways-to-lie-with-charts/)]
]

---

## Tendencias

* Existen distintos métodos de suavizado para representar la tendencia

* Uno de los más populares es LOESS (*locally estimated scatterplot smoothing*)

---

También es útil usar estos métodos de suavizado en gráficos de dispersión

---

## Funciones de suavizado

Cuidado al interpretar los datos suavizados, pueden cambiar bastante dependiendo del método!

---

## Regresión lineal

Es muy común superponer la recta de regresión para comprobar visualmente si dos variables tienen relación lineal

---

# Otros tipos de gráficos

---

## Más gráficos

* Hemos visto los más comunes, pero hay muchos más:
  
   * Datos geoespaciales

* Gráficos cuantil-cuantil

* Gráficos mosaico

* Mapas en árbol

* Conjuntos paralelos

* etc.

* Un buen directorio: [From Data to Viz](https://www.data-to-viz.com/)

---

## Ratio datos-tinta

* Concepto introducido por Edward Tufte en 1983

* Sin importar el tipo de gráfico, tiene que ser estéticamente agradable para no distraer del mensaje a transmitir

* Consiste en maximizar la proporción de los elementos estéticos del gráfico que se usan para visualizar datos

.center[
<iframe width="560" height="315" src="https://www.youtube.com/embed/bDbJBWvonVI" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
]

---