class: center, middle, inverse, title-slide # Aprendizaje profundo ## Curso de aprendizaje automático para el INE ### Alberto Torres y Víctor Gallego ### 2019-06-05 --- class: middle, center, inverse # Introducción --- ## Repaso de Deep Learning * Modelo principal: red profunda (**feed-forward**): composición de **proyecciones lineales** y **no-linealidades** `\begin{align} h^{(i+1)} &= Wz^{(i)} + b \\ z^{(i+1)} &= \sigma (h^{(i+1)}) \\ \end{align}` * Al final: añadir coste apropiado para regresión o clasificación. * Las redes neuronales se conocen desde mediados del siglo XX, pero su fuerte resurgimiento no fue hasta esta década: * Paralelización en tarjetas gráficas (**GPUs**). * Librerías de **diferenciación automática**. --- ## Diferenciación Automática (AD) (1) * ¿Cómo calcular el gradiente en una red profunda? -- * **A mano**: no escala a nuevas arquitecturas, propenso a errores. * **Diferenciación numérica**: acumulación de errores y elevado coste computacional. `\begin{equation} \frac{\partial E_n}{\partial w_{ji}} = \frac{E_n(w_{ji} + \epsilon) - E_n(w_{ji} - \epsilon)}{2 \epsilon} + O(\epsilon^2) \end{equation}` * **Diferenciación simbólica**: manipulación exacta de expresiones (mediante tablas de derivadas), pero explosión en la cantidad de términos: <center>  </center> --- ## Diferenciación Automática (AD) (2) * Surge la **diferenciación automática o algorítmica**: aplica diferenciación simbólica pero solo a expresiones simples, y al componerlas, actualiza los resultados numéricos parciales (que serán **exactos**) * Ejemplo para calcular la derivada de `\(y = f(x_1, x_2) = \log (x_1) + x_1 x_2 - \sin (x_2)\)` en `\((x_1, x_2) = (2, 5)\)`: <center>  </center> --- ## Diferenciación Automática (AD) (3) * ¿Por qué **backpropagación**? * Ejemplo: considera una serie de funciones `\(f : \mathbb{R}^n \rightarrow \mathbb{R}^m\)`, `\(g : \mathbb{R}^m \rightarrow \mathbb{R}^m\)` y `\(h : \mathbb{R}^m \rightarrow \mathbb{R}\)`. Queremos obtener la derivada de su composición, `\(\frac{\partial (h \circ g \circ f)}{\partial x}\)` * Queda que `\begin{equation} \frac{\partial (h \circ g \circ f)}{\partial x} = \frac{\partial h}{\partial g} \frac{\partial g}{\partial f} \frac{\partial f}{\partial x} \end{equation}` * Asociando `\(\frac{\partial h}{\partial g} ( \frac{\partial g}{\partial f} \frac{\partial f}{\partial x} )\)`, queda un producto matriz-matriz y otro producto vector-matriz. * Asociando `\(( \frac{\partial h}{\partial g} \frac{\partial g}{\partial f} )\frac{\partial f}{\partial x}\)`, ¡solo hay que hacer productos vector-matriz!: mucho más eficiente. -- * En ML es habitual optimizar funciones de tipo `\(\mathbb{R}^d \rightarrow \mathbb{R}\)`, por tanto es más eficiente propagar los gradientes hacia atrás (**backpropagation**) que hacia adelante (**forward propagation**). --- ## Optimizando mediante SGD o Adam. * Una vez hemos calculado el gradiente en un punto mediante AD, las opciones actuales más populares son * **Descenso por el gradiente estocástico** (SGD): ya visto, estimación usando mini-batches. * **Adam** (2014: https://arxiv.org/abs/1412.6980) : corrige el gradiente estimando una ventana móvil de su media y de su varianza. <center>  </center> --- ## Volviendo a Deep Learning * Ya tenemos todos los ingredientes: * Datasets enormes. * Redes neuronales como **aproximadores universales**. * Librerías para **diferenciación automática**: tensorflow, keras, pytorch... * Potentes CPUs o GPUs para **paralelizar a lo largo de cada ejemplo del mini-batch**. * ¿Qué falta en muchas ocasiones? -- * Solo teóricamente las redes neuronales son totalmente expresivas. * Conviene añadir un **sesgo inductivo** (**inductive bias**) para ayudar al aprendizaje: * Imágenes, señales: invarianza a traslaciones, escala: **redes convolucionales**. * Texto, secuencias: sensibilidad al orden de los símbolos: **redes recurrentes**. --- class: middle, center, inverse # Redes recurrentes (RNNs) --- ## Intuición * Las redes neuronales recurrentes (*recurrent neural networks*, RNNs) surgen de la necesidad de **procesar secuencias** de datos (fundamentalmente textos). * ¿Qué hacemos cuando los inputs pueden tener diferentes longitudes? -- * **Idea** añadir conexiones a modo de feedback (<span style="color:green"> `\(\rightarrow\)` </span>) <center>  </center> --- ## Esquema original * Modelo de **Elman**: la red mantiene un estado interno `\(h_t\)` que se va actualizando en cada iteración `\begin{equation} h_t = f_W ( h_{t-1}, x_t) \end{equation}` * En concreto, un posible diseño es `\begin{align} h_t &= \tanh (W_{hh}h_{t-1} + W_{xh}x_t) \\ y_t &= W_{hy} h_t \end{align}` * Los **pesos se reutilizarn en cada instante `\(t\)`**: * aprende patrones independientemente de su posición. * reducción en el número de parámetros. * Podemos desarrollar la recurrencia a lo largo de `\(t\)` (ver siguientes): --- ## Grafo computacional * Ejemplo de arquiectura **many-to-one** (ej: asignar sentimiento (+ ó -) a un tweet (secuencia de palabras)) <center>  </center> --- ## Grafo computacional * Ejemplo de arquiectura **many-to-many** (ej: predicción de una señal: en cada `\(x_t\)` predecimos `\(x_{t+1}\)` con el valor `\(y_t\)`)) <center>  </center> --- ## Ejemplo (many to many) * Predicción del siguiente carácter. * Representamos cada carácter mediante OHE, nuestro vocabulario es: h, e, l, o `\(\in \lbrace 0, 1 \rbrace^4\)`. <center>  </center> --- ## Entrenamiento * Mismo esquema de backpropagación que para las redes estándar, solo que ahora se propaga hacia atrás en el tiempo (como si la RNN estuviera desenrrollada). * Para mejorar la estabilidad, solo se propaga hacia atrás un número de pasos limitado (**truncated backpropagation**) * SGD o Adam. <center> 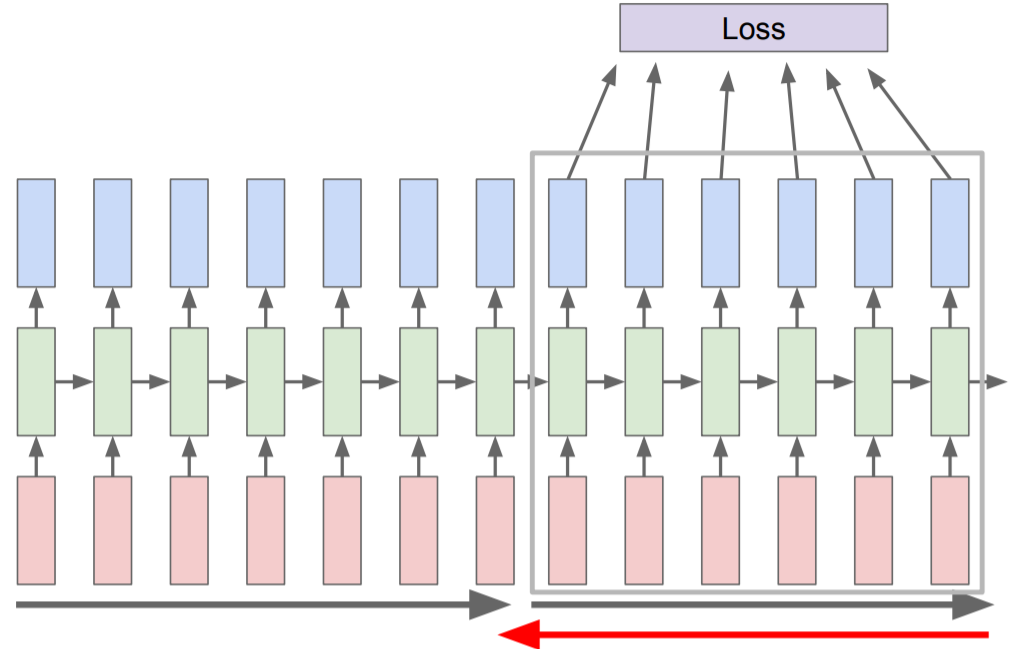 </center> --- ## Problema de la RNN original (1) * La backpropagación desde `\(h_t\)` a `\(h_{t-1}\)` necesita multiplicar por `\(W\)`. <center> 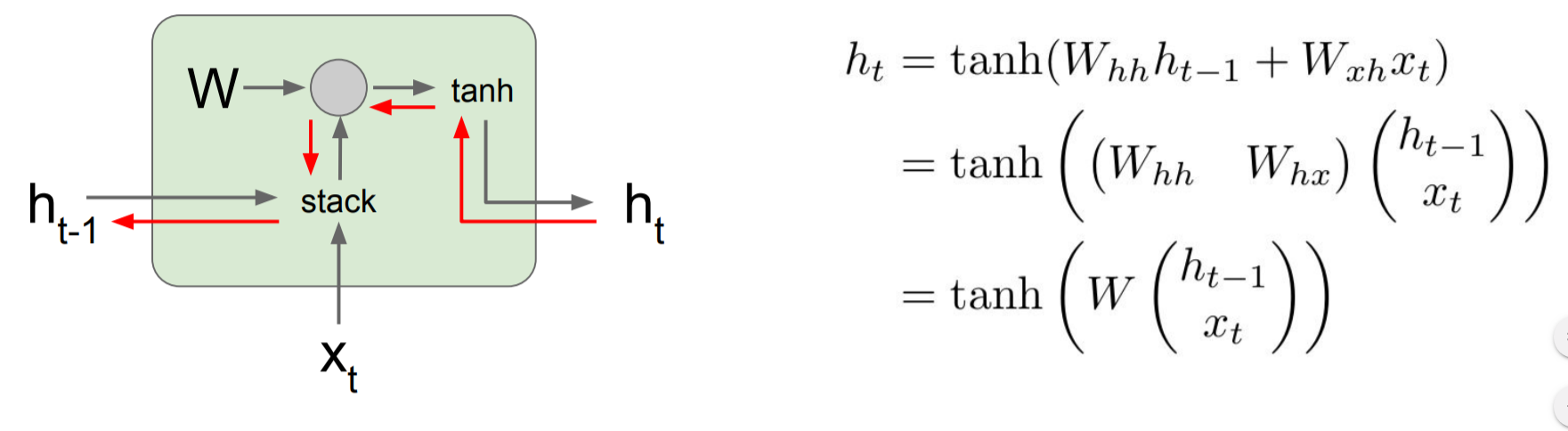 </center> * Al hacerlo a lo largo del tiempo: <center>  </center> * Calcular el gradiente para `\(h_0\)` implica multiplicaciones de `\(W\)`. --- ## Problema de la RNN original (2) * Calcular el gradiente para `\(h_0\)` implica multiplicaciones de `\(W\)`: * El mayor valor singular (autovalor) de `\(W\)` es `\(> 1\)`: explosión del gradiente. * Solución: acotar manualmente el gradiente (**gradient clipping**). * El mayor valor singular (autovalor) de `\(W\)` es `\(< 1\)`: desvanecimiento del gradiente. * Solución: nueva arquitecturas (LSTM, GRU). --- ## Long-Short Term Memory network (LSTM) * Introducidas por Hochreiter en 1997, aunque no se usaron mucho hasta esta década (aplicaciones en NLP). * Añadimos un nuevo estado (cell, `\(c_t\)`) y varias compuertas (gates) para mejorar el flujo del gradiente. <center> 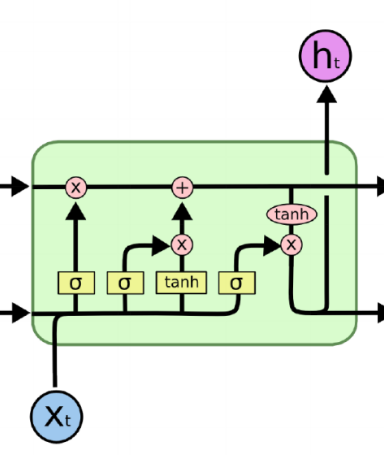 </center> --- ## LSTM (2) * Compuerta de **olvido** (forget). * Decide qué partes olvidar del estado anterior. <center> 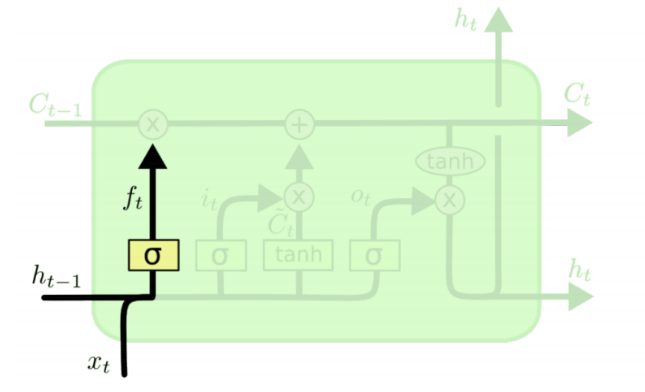 </center> `\begin{equation} f_t = \sigma (W_f \left[ h_{t-1}, x_t \right] + b_f) \end{equation}` --- ## LSTM (3) * Compuerta de **actualización** (update). * Decide qué modificar para el nuevo estado. <center>  </center> `\begin{align} i_t &= \sigma (W_i \left[ h_{t-1}, x_t \right] + b_i) \\ \tilde{C}_t &= \tanh (W_C \left[ h_{t-1}, x_t \right] + b_C) \end{align}` --- ## LSTM (4) * Compuerta de **salida** (output) <center>  </center> `\begin{align} o_t &= \sigma (W_o \left[ h_{t-1}, x_t \right] + b_o) \\ h_t &= o_t * \tanh (C_t) \end{align}` --- ## LSTM en resumen * Las ecuaciones completas son <center>  </center> * Ahora para hacer backpropagación de `\(c_t\)` a `\(c_{t-1}\)` no hace falta multiplicar por `\(W\)`!! <center>  </center> --- ## Resumen * Las RNNs permiten gran flexibilidad en el diseño de la arquitectura. * Las RNNs originales son simples pero no funcionan bien. * Más común: utilizar **LSTM** para "mejorar" el gradiente. * El flujo de gradiente hacia atrás puede explotar o desvanecerse en las RNNs: la **explosión** se controla acotando el gradiente (clipping). El **desvanecimiento** mediante conexiones aditivas (LSTM). * Las búsqueda de arquitecturas más simples es área de investigación actual. * Todavía hay escasos avances teóricos, se necesita más investigación. * Las **gated recurrent units** (GRU) son algo más sencillas aunque siguen el mismo mecanismo de compuertas (https://www.aclweb.org/anthology/D14-1179) --- class: middle, center, inverse # Aplicación de RNNs a Procesamiento de Lenguaje Natural --- ## Cambio de paradigma * Pre 2000s: **simbólico, basado en reglas** * Lenguaje entendido como conjunto de elementos y reglas para combinarlos. * Gramáticas independientes de contexto (Chomsky). * Más adecuado a lenguajes artificiales (de programación) que naturales (humanos). <center>  </center> * Después: **estadístico, basado en datos** * Lenguaje entendido como probabilidades de secuencias de palabras. * Cálculo de frecuencias de palabras, n-gramas, etc. * Más adecuado a lenguajes naturales que artificiales. * Combinación con modelos profundos: **estado del arte**. --- ## De n-gramas a word embeddings (1) * **Bag of words**: contamos la aparición (o frecuencia) de cada palabra: <span style="color:blue">El atento alumno `\(\rightarrow\)` (El), (atento), (alumno)</span>. * Representaríamos la frase como $$ \left(0 , \ldots, 1, 0, \ldots, 0, 1, 0, \ldots, 1, 0 \right) \in \lbrace 0, 1 \rbrace^{|V|} $$ * donde `\(|V|\)` es el número de palabras de nuestro vocabulario `\(V\)`. * Problema: no tiene en cuenta el orden (y contexto) de las palabras. Solución (parcial): * **2-gramas**: contamos ahora pares consecutivos de palabras: <span style="color:blue">(El, atento), (atento, alumno)</span>. * Ahora la representación es sobre `\(\lbrace 0, 1 \rbrace^{|V|^2}\)`. -- * **n-gramas**: explosión combinatoria... * Ha sido lo estándar hasta `\(\sim 2013\)`. ¿Podemos encontrar una representación más compacta? --- ## De n-gramas a word embeddings (2) * Cada palabra (representada mediante OHE) se mapea a un espacio continuo: `\(\lbrace 0, 1 \rbrace^{|V|} \rightarrow \mathbb{R}^m\)`. * Mediante una transformación lineal `\(z_i = E w_i\)` donde `\(E\)` es una matriz de tamaño `\(m \times |V|\)`. Típicamente `\(m = 300 << |V|\)`. <center>  </center> * **Combaten la catástrofe de la dimensionalidad**, mediante una compresión de los datos, pasando de un espacio discreto a uno continuo. * Al proyectar a un espacio continuo, esperamos que palabras parecidas (sinónimos) se encuentren cerca (bajo la métrica euclidea). --- ## Álgebra lineal en el espacio de palabras (1) * **One-hot encoding**: no hay noción de vecindad entre palabras, cualquier palabra está igual de lejos que las demás. * **Word embeddings** (codificación densa): podemos usar la distancia euclídea (u otras) en `\(\mathbb{R}^m\)`. <center>  </center> --- ## Álgebra lineal en el espacio de palabras (2) * Como estamos en un espacio vectorial ( `\(\mathbb{R}^m\)` ), podemos realizar operaciones con vectores (word embeddings). * Aprenden ciertas analogías entre palabras. <center>  </center> --- ## word2vec (2013) * La pregunta del millón: **¿cómo obtener la matriz `\(E\)` de word embeddings?** -- * Basado en la **hipótesis distribucional** del lenguaje (J. Firth 1957): el significado de una palabra puede inferirse a partir del contexto (palabras vecinas en las que aparece) * El modelo word2vec presenta dos variantes: * **CBoW**: dado un contexto, predecir palabra central. * **Skip-gram**: dada la palabra central, predecir el contexto. <center>  </center> --- ## Uso de embeddings preentrenados * Aunque los embeddings pueden inicializarse aleatoriamente (como los pesos de una red neuronal estándar) y aprenderse durante la tarea, * Una técnica habitual es cargar unos **word embeddings preentrenados**, para ahorrar tiempo y datos. * Una vez ya tenemos los embeddings, se los acoplamos a cualquier modelo (regresión logística, red neuronal) y procedemos con el entrenamiento. * https://fasttext.cc/ mejora de word2vec (contiene información de prefijos y sufijos). * https://fasttext.cc/docs/en/crawl-vectors.html en castellano, entrenados sobre los artículos de la Wikipedia y CommonCrawl. --- ## Generación de textos * https://openai.com/blog/better-language-models/ * GPT-2 es un modelo de lenguaje entrenado sobre un corpus de 40GB de datos (8 millones de páginas webs). * La versión grande del modelo consta de 1500 millones de parámetros. * Generación de historias online en https://talktotransformer.com/ --- ## Traducción automática * Modelos **seq2seq**: composición de many-to-one + one-to-many. * `\(x_1, \ldots, x_T\)` es la frase en el idioma original. * `\(y_1, \ldots, y_{T'}\)` es la frase en el idioma de destino. <center>  </center> * Sequence to Sequence Learning with Neural Networks: https://arxiv.org/abs/1409.3215 * Actualmente usado en **Google Traslate**: https://ai.google/research/pubs/pub45610 --- ## Subtitulación de imágenes <center>  </center> * Explain Images with Multimodal Recurrent Neural Networks: https://arxiv.org/pdf/1410.1090.pdf * Show and Tell: A Neural Image Caption Generator: https://arxiv.org/pdf/1411.4555.pdf --- class: middle, center, inverse # Redes convolucionales --- ## Introducción * Tipo de red neuronal para datos con topología similar a una rejilla 1. 1D, series temporales, audio 2. 2D, imágenes, datos espaciales 3. 3D, video, datos espacio-temporales, meteorología * Red convolucional: en al menos una capa se usan convoluciones en lugar de operaciones con matrices --- ## Competición ImageNet * Más de 14 millones de imágenes anotadas a mano * Más de 20,000 categorias * Desde 2010, competición anual de clasificación automática (ILSVRC) * únicamente 1000 categorias * en 2011, el mejor error era de aprox. 25% * en 2017, 29/38 equipos tenían un error menor del 5% --- ## Historia 1. En 1990, [Lecun et al.](http://yann.lecun.com/exdb/publis/pdf/lecun-90c.pdf) usa una CNN para leer dígitos de códigos postales * una de las primeras aplicaciones reales de una red neuronal * más del 90% de tasa de acierto 2. En 2012, [Krizhevsky et al.](https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf) usan una CNN para ganar la competición ILSVRC2012 * tasa de acierto (top 5), 15.3% * segundo mejor modelo, 26.2% 3. A partir de 2012 múltiples arquitecturas más complejas siguen reduciendo el error: * 2014: VGG-16 (7.3%), GoogleNet (6.7%) * 2015: Microsoft ResNet (3.57%) --- ## Conexiones densas (*fully connected*) .center[  ] --- ## Conexiones *sparse* (*locally connected*) .center[  ] --- ## Convolución en 2D * `\(I\)` es la matriz de entrada (2D) * `\(K\)` es el kernel (2D) `$$S(i, j) = (K * I)(i,\, j) = \sum_m \sum_n I(i+m,\, j+n) K(m,\, n)$$` * La convolución o filtro se aplica a toda la imágen con los mismos pesos * Se define con 4 parámetros: * *stride* o paso de la convolución * tamaño del kernel, generalmente cuadrado * *depth*, número de filtros o convoluciones distintas a aplicar * *padding* --- ## Ejemplo .center[  [Goodfellow et al. Deep Learning (2016)](https://www.deeplearningbook.org/) ] --- # Motivación 1. conexiones dispersas * explotar estructura espacial * detectar características locales (aristas, etc.) 2. compartición de pesos * invariante frente a traslaciones * reduce la cantidad de memoria necesaria --- ## Ejemplo características locales  * Imagen de la derecha: restar a cada píxel su vecino por la izquierda * Esta operación se puede representar de forma muy eficiente con una convolución --- ## *Stride* (paso) .center[  [Fuente](https://adeshpande3.github.io/A-Beginner%27s-Guide-To-Understanding-Convolutional-Neural-Networks-Part-2/)] --- ## Ejemplos .pull-left[ * Entrada `\(4 \times 4\)` * Kernel `\(3 \times 3\)` * Stride 1 * Salida `\(2 \times 2\)`  ] .pull-right[ * Entrada `\(5 \times 5\)` * Kernel `\(3 \times 3\)` * Stride 2 * Salida `\(2 \times 2\)`  ] --- ## Padding * En ocasiones se añade un *padding* de 0 al borde de la imágen: 1. preservar el tamaño de la entrada 2. cuando es necesario por la combinación de tamaño de entrada, tamaño de kernel y stride * Ejemplo: entrada `\(5\times 5\)`, kernel `\(3 \times 3\)` y *stride* 2 .center[  [Fuente](http://deeplearning.net/software/theano/tutorial/conv_arithmetic.html)] --- * Generalmente la salida tiene menor tamaño que la entrada * Aplicando padding podemos hacer que tenga el mismo o incluso mayor * Entrada `\(5 \times 5\)`, stride 1, kernel `\(3 \times 3\)` .pull-left[  .center[ Salida `\(5 \times 5\)` ] ] .pull-right[  .center[ Salida `\(7 \times 7\)` ] ] --- * A veces el padding es necesario para poder aplicar el kernel * Ejemplo: kernel `\(3 \times 4\)`, stride 2 * La salida tiene el mismo tamaño en ambos! .pull-left[  .center[ Entrada `\(5\times 5\)` ] ] .pull-right[  .center[ Entrada `\(6 \times 6\)` ] ] --- ## Pooling * Capa de submuestreo no lineal * Previene sobreajuste, reduciendo número de parámetros * Ayuda con la invarianza frente a traslaciones * Útil cuando interesa conocer si una característica está o no, pero no su localización exacta `\(\Rightarrow\)` clasificación imágenes * Más habitual: **max pooling** -- ![:vspace 1] .center[  ] --- ## Arquitectura típica * Parámetros: número de *feature maps*, tamaño del kernel, stride * Subsampling: max pooling * Antes de las capas *fully connected*, hay que aplanar (*flatten*) la salida ![:vspace 5]  --- ## Visualizando activaciones .center[   ] --- ## Primeras capas  --- ## Últimas capas  --- ## CAM (class activation map)  --- ## Ejemplo arquitectura: AlexNet  ```r model <- keras_model_sequential() %>% layer_conv_2d(filters = 96, kernel_size = c(11, 11), activation = 'relu', input_shape = c(224, 224, 3), strides = c(4, 4), padding = 'valid') %>% layer_max_pooling_2d(pool_size = c(2, 2), strides = c(2, 2), padding = 'valid') %>% ... ``` --- class: middle, center, inverse # Recursos adicionales --- ## Enlaces de interés * https://reddit.com/r/LearnMachineLearning: nivel introductorio/medio * https://reddit.com/r/machinelearning: discusiones sobre artículos y temas de actualidad * https://medium.com/topic/machine-learning: artículos hacia audiencia general