Redes neuronales

# Redes neuronales
## Curso de aprendizaje automático para el INE
### Alberto Torres Barrán y Roi Naveiro
### 2019-06-04

---

---
class: middle, center, inverse

# Introducción
---

## Perceptrón

* Combinación lineal de las variables de entrada

* No linealidad: función de activación (por ejemplo la función escalón)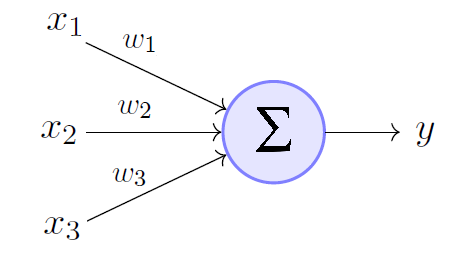

[Fuente](https://towardsdatascience.com/perceptron-the-artificial-neuron-4d8c70d5cc8d)
]
---

## Ejemplo perceptron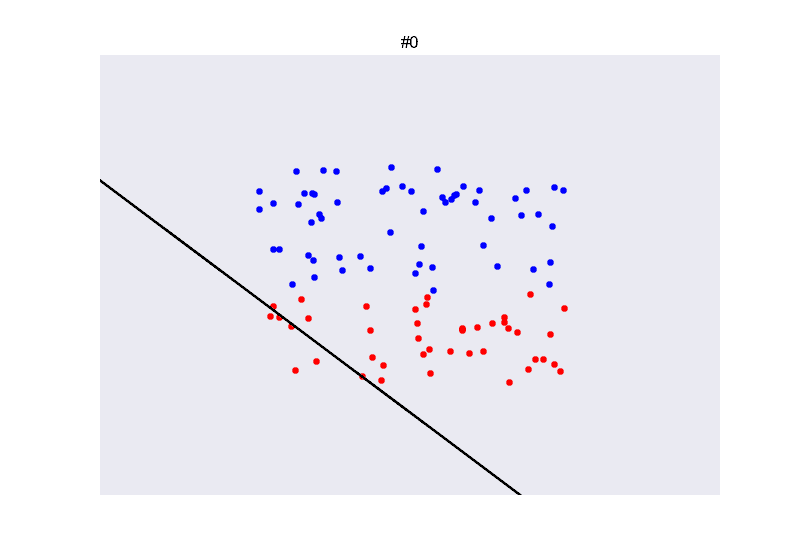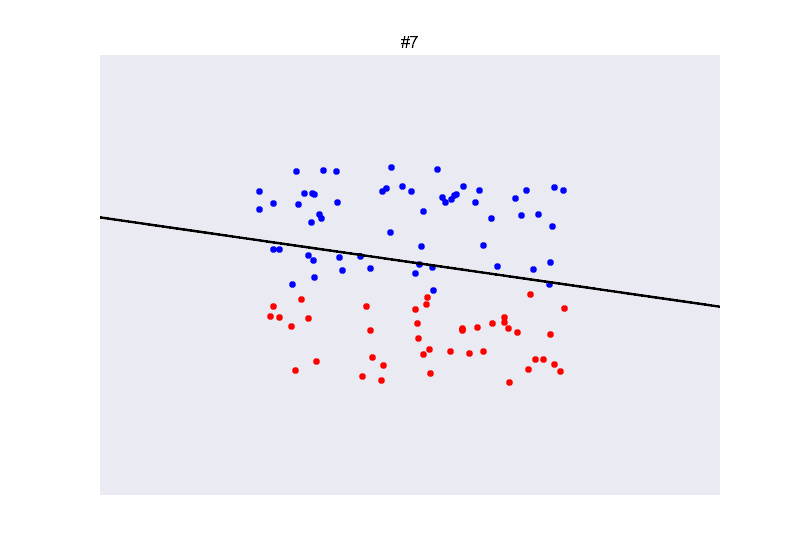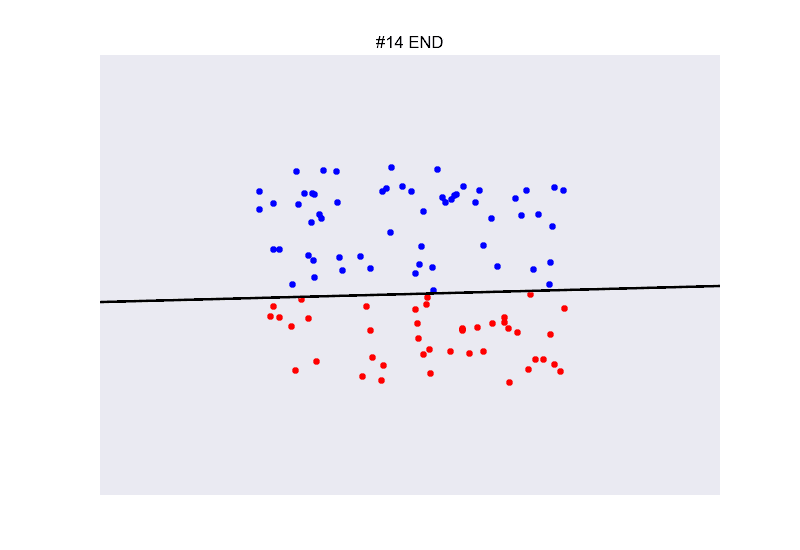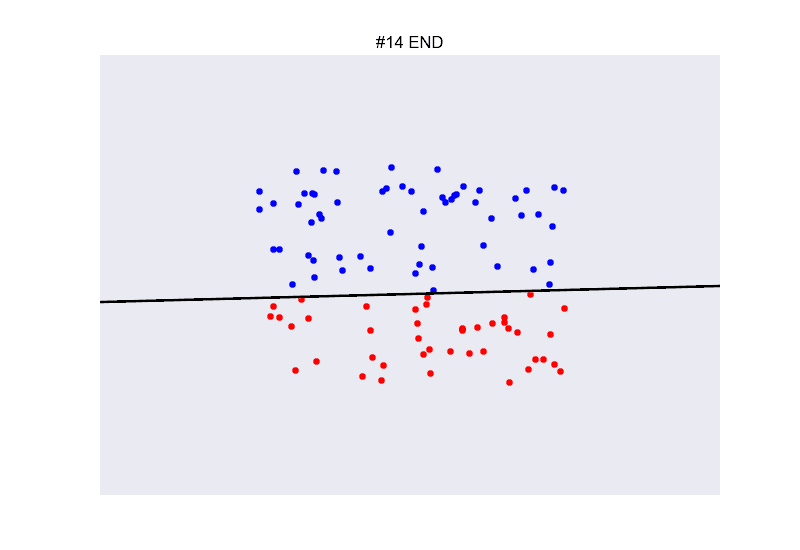

[
![](https://raw.githubusercontent.com/miku/nntour/master/gifs/perceptron-pla-14-steps.gif)](https://github.com/miku/nntour)

---

## Problema XOR

* Observaciones no separables linealmente `$\Rightarrow$` perceptrón no encuentra solución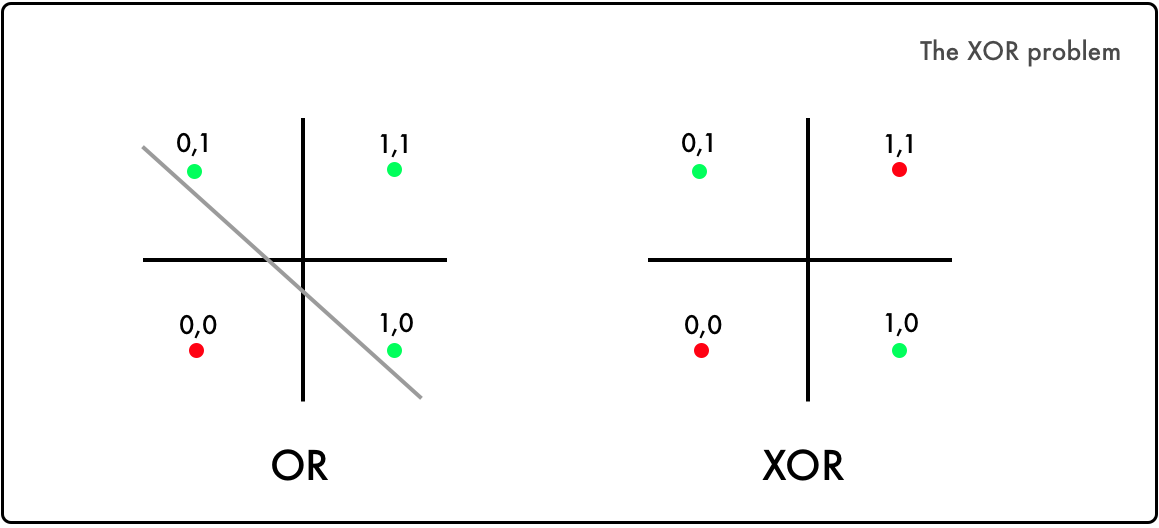

[Fuente](https://www.freecodecamp.org/news/the-history-of-deep-learning-explored-through-6-code-snippets-d0a0e8545202/)
]
---

## Redes neuronales

* Añadimos una capa intermedia (capa oculta)

[Fuente](https://en.wikipedia.org/wiki/Artificial_neural_network)
]

---

## Teorema de aproximación universal

* Asumimos:

- red neuronal feed-forward
  
  - una capa oculta
  
  - número de neuronas finito
  
  - algunas funciones de activación (por ej. sigmoidea)
  
* Aproxima cualquier función continua con precisión arbitrarea

* **Pero**:el número de neuronas necesario es exponencialmente grande

---

## Aprender representaciones

* Modelos como las SVMs generan una nueva representación de los datos de entrada en un espacio ampliado

* Esperamos que en este nuevo espacio el problema de aprendizaje sea más sencillo

* Esta nueva representación también se puede generar de forma manual (*feature engineering*)

* Crear nuevas variables es, típicamente:

1. critico para obtener buen rendimiento
  
  2. muy dependiente del problema
  
* Ejemplo: extraer variables de datos no tabulares (audio, video, imágenes, texto)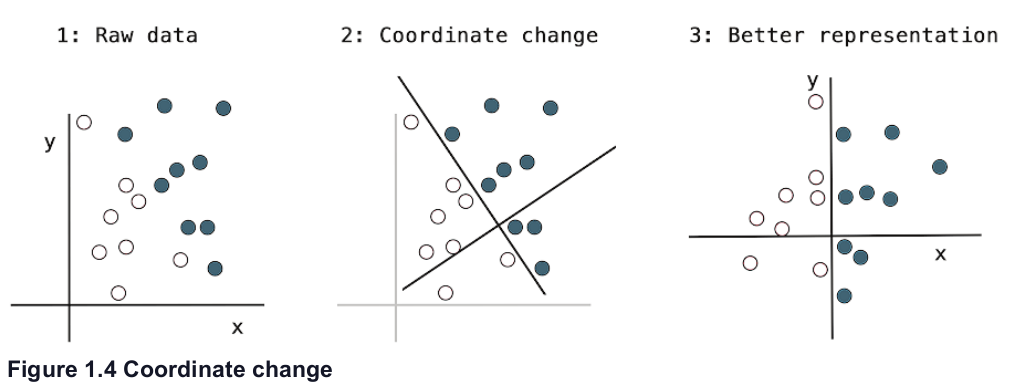

---

![](./img/coordinate_change.png)

---

## RN vs otros modelos
  
* Automatizan la creación de nuevas variables

* Esto simplifica la resolución de nuevos problemas:
  
  1. no necesario tanto conocimiento específico 
  
  2. proceso mucho menos costoso que crear nuevas variables a mano
  
* Además la creación de estas nuevas representaciones forma parte del aprendizaje

* específicas para la tarea a resolver `$\Rightarrow$` mejor rendimiento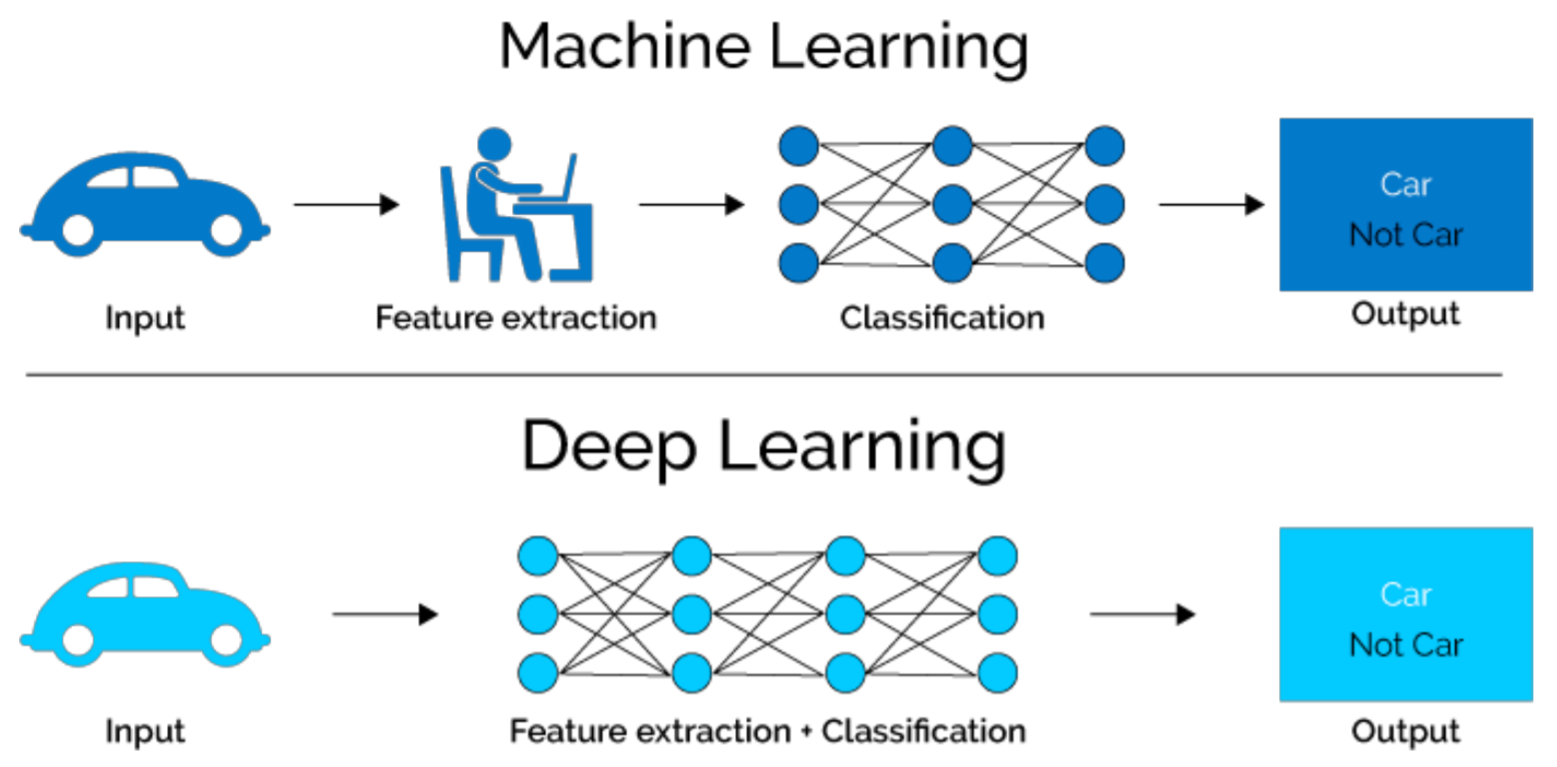
  
---

![](img/nn_vs_rest.png)
  
---

## Ejemplo

* Clasificar imágenes médicas en sano/enfermo

* Antes: una parte importante del trabajo consistía en procesar las imágenes del microscopio para extraer características:

1. segmentar células
  
  2. identificar núcleo
  
  3. etc.
  
* Redes neuronales profundas extraen automáticamente características **útiles para la tarea de clasificar**

---

## ¿Por qué ahora?

* Redes convolucionales y *backpropagation* son de 1989

* Redes recurrentes como la LSTM de 1997

* Desde 2010 varios avances han contribuido al exíto de las redes neuronales:

1. hardware
  
  2. datos
  
  3. avances algorítmicos
  
---

## Hardware

* Entre 1990 y 2010 las CPUs estándar incrementaron su velocidad un factor de 5000

* Modelos de redes neuronales entrenables en un portátil estándar

* No suficiente para modelos más complejos (recurrentes, convolucionales)

* GPUs: unidades de procesamiento gráfico

1. procesadores más sencillos
  
  2. útiles para procesar grandes bloques de datos en paralelo
  
* Entrenar una red necesita muchas multiplicaciones de matrices

* NVIDIA Titan X (aprox. 1000$) tiene 350 veces más potencia que un portátil moderno `$\Rightarrow$` 6.6 trillones de operaciones en coma flotante/segundo

---

## Datos

* Desarrollo exponencial de la capacidad de almacenamiento

* Internet: recolectar y distribuir conjuntos de datos de forma sencilla

1. Wikipedia (texto)
  
  2. Youtube (video)
  
  3. Flickr (imágenes)
  
* Competiciones de benchmark, por ej. ImageNet o Kaggle

---

## Algoritmos

* Hasta 2010 no existían formas fiables de entrenar redes neuronales profundas (solo 1 o 2 capas)

1. se puede calcular el gradiente (*backpropagation*)

2. la señal del error se desvanece en las capas intermedias

* Ciertos avances algorítmicos aliviaron el problema:

1. mejores funciones de activación
  
  2. mejor inicialización de los pesos

3. mejores algoritmos de optimización (variantes de SGD)
  
* Se pueden entrenar redes con 10 o más capas

* Hoy en día otros avances permiten entrenar modelos con cientos de capas
  
---

## Ventajas y desventajas

Ventajas

* Simplicidad: no es necesario crear nuevas variables a mano

* Escalabilidad: 
  
  1. paralelizacion en GPUs
  
  2. uso de mini-baches

* Versatilidad y reusabilidad:
  
  1. aprovechar representaciones aprendidas para otros problemas
  
  2. continuar el entrenamiento con nuevos datos
  
Desventajas

* Coste computacional y hardware

* Dificultad entrenamiento

---

## Democratización

* Antes: programar en GPUs `$\Rightarrow$` lenguajes específicos (CUDA) y C++

* Desde 2010: multiples librerias (Torch, Theano, Caffe, Tensorflow) que

1. realizan diferenciación automática
  
  2. implementan tensores y operaciones con los mismos
  
  3. hacen uso de la GPU de forma transparente

* Ahora: varias librerías de alto nivel que implementan capas de aprendizaje profundo:

1. **Keras**
  
  2. PyTorch
  
---

## Ejemplo Keras

* Problema de regresión con 2 salidas

* Arquitectura:

---

```r
library(keras)

model <- keras_model_sequential()

# arquitectura
model %>% 
  layer_dense(units = 4, 
              activation = 'sigmoid', 
              input_shape = c(3)) %>% 
  layer_dense(units = 2, 
              activation = 'linear')

# definir entrenamiento
model %>% compile(loss = "mse", 
                  optimizer = optimizer_sgd())

# entrenamiento
model %>% fit(X_train, y_train, 
              epochs = 10, batch_size = 128, 
              validation_size = 0.2)

# error de test
model %>% evaluate(X_test)
```
  
---

---

## Introducción

* Hasta ahora hemos visto modelos de regresión y clasificación que recibían como input combinaciones lineales de *funciones base*.

* Para que estos modelos resulten prácticos, debemos adaptar las funciones base a los datos.

* Idea:

1. Fijar el número de funciones base de antemano
  
  2. Darles forma paramétrica
  
  3. Aprender parámetros usando los datos.

* **Aprender la representación**.

* *Perceptrón multicapa* o *feed-forward neural network*.

---

## Perceptrón multicapa (1)

* ¿Cómo parametrizamos las funciones de base?

* Hasta ahora

`\begin{equation}
y(x,w) = f \left( \sum_{j=1}^M w_j \phi_j(x) \right)
\end{equation}`

* Siendo `$f$` una **activación no lineal**.

* Objetivo: parametrizar `$\phi_j(x)$` y aprender los parámetros.

* Idea de las NN: parametrizar `$\phi_j(x)$` de la misma manera que `$y(x,w)$`.

---

## Perceptrón multicapa (2)

* MLP básico:

1. Construír `$M$` combinaciones lineales del input `$x_1, \dots, x_D$`:
`\begin{equation}
a_j = \sum_{i=1}^D w_{ji}^{(1)} x_i + w_{j0}
\end{equation}`
  
  2. Transformar cada activación `$a_j$` usando una función de activación **no lineal** y **diferenciable**: `$z_j = h(a_j)$`.
  
  3. Repetir 1 y 2, tantas veces como **capas ocultas** queramos en la red.
  
  4. Por último, en la capa de salida, las activaciones se transforman con una función de activación adecuada para producir los outputs `$y_k$`.

* Notación: `$w_{ji}$` son *pesos*, `$w_{j0}$` son *biases*, `$a_j$` son *activaciones*.

---

## Perceptrón multicapa (3)

* **Ejercicio**: ¿Por qué las activaciones tienen que ser funciones no lineales diferenciables?

---

## Perceptrón multicapa (4)
  
* La función de activación de la capa de salida, dependerá de la naturaleza de los datos.

* Para problemas de regresión, la activación será la identidad `$y_k = a_k$`.

* Para clasificación binaria (output es una probabilidad) la activación será la sigmoide `$y_k = \sigma(a_k)$`.

* Para clasificación multiclase, usaremos la softmax.

`\begin{equation}
\text{softmax}(a)_i = \frac{e^{a_i}}{\sum_k e^{a_k}}
\end{equation}`

---

## Perceptrón multicapa (5)

* ¿Funciones de activación de capas intermedias?

* Históricamente, la sigmoide.

* Hoy en día, las más conocidas son la *REctifier Linear Unit (RELU)*, tangente hiperbólica y variantes.

<center>
![:scale 100%](./img/activation.png)
</center>

---

## Perceptrón multicapa (6)

* Componiendo lo visto, obtenemos una NN de dos capas (e.g. con salida binarias)

`\begin{equation}
y(w,x) = \sigma \left( \sum_{j=0}^M w_{j}^{(2)} h \left( \sum_{i=0}^D w_{ji}^{(1)} x_i\right) \right)
\end{equation}`

* El proceso de evaluar esta función se denomina *forward propagation*.
.center[
![:scale 60%](./img/neuron.svg)

[Fuente](https://victorzhou.com/blog/intro-to-neural-networks/)
]

---

## Perceptrón multicapa (7)

* Gráficamente...

<center>
![:scale 100%](./img/nn.jpg)
</center>

---

---

## Entrenamiento de la red

* Para entrenar, necesitamos definir función objetivo (función de coste).

* Una opción: **mínimos cuadrados**.

* Si damos **interpretación probabilística** a la salida de la NN, conseguimos una visión más general.

---

## Regresión

* Asumiremos que el target `$t$` sigue una distribución normal

`\begin{equation}
p(t \vert y(x,w), \beta^{-1})
\end{equation}`

* Donde la activación de la capa de salida es la identidad.

* Dado conjunto de entrenamiento `$X = \lbrace x_1, \dots, x_N \rbrace$`, `$\boldsymbol{t} = t_1, \dots, t_N$`, maximizar la verosimilitud es equivalente a

`\begin{equation}
w_{ML} = \arg\min_w E(w) = \arg\min_w \frac{1}{2} \sum_{i=1}^N \lbrace y(x_n,w) - t_n\rbrace^2
\end{equation}`

* Ojo: la **no linealidad** de la red hace que `$E(w)$` no sea convexo... en la práctica conseguiremos converger a mínimo local.

* En regresión multi-target, se asume **independencia condicional** de los targets dados `$x$` y `$w$` y el análisis es idéntico.

---

## Clasificación binaria

* `$t=1$` representa una pertenencia a una clase y `$t=0$` a la otra. La NN tiene una única salida con activación sigmoide.

* Interpretamos `$y(x,w)$` como `$p(t=1 \vert x )$`. Entonces

`\begin{equation}
p(t \vert x,w) = y(x,w)^t \lbrace 1-y(x,w) \rbrace^{1-t}
\end{equation}`

* Dado conjunto de entrenamiento, maximizar la verosimilitud equivale a minimizar la **entropía cruzada**

`\begin{equation}
E(w) = - \sum_{n=1}^N \lbrace t_n \log y_n + (1-t_n) \log (1-y_n) \rbrace
\end{equation}`

* Para clasificación binaria **multi-etiqueta**, usamos una red con `$K$` outputs sigmoidales.

* Asumiendo independencia condiciones de las etiquetas dado el input, el análisis es idéntico.

---

## Clasificación multiclase

* Las `$K$` posibles clases se escriben en notación One-Hot-Encoding.

* Si la observación `$n$`-ésima, pertenece a la clase 1, entonces `$t_{n1}=1$` y `$t_{nj} = 0$` para `$j \neq 1$`.

* La red tiene `$K$` salidas interpretadas como `$y_k(x,w) = p(t_{\cdot k} = 1 \vert x)$`.

* Maximizar la verosimilitud equivale a minimizar

`\begin{equation}
E(w) = - \sum_{n=1}^N \sum_{k=1}^K t_{nk} \log y_k(x_n,w)
\end{equation}`

* La red tiene `$K$` unidades de salida con activación softmax.

---

## Optimización

* Una vez definida la función de coste, hay que encontrar los pesos que la optimicen.

* `$\nabla E(w) = 0$` no se puede resolver analíticamente. Tenemos que usar métodos numéricos iterativos.

* Los más importantes: **basados en el gradiente**, pues como veremos, evaluar el gradiente es muy eficiente gracias al algoritmo de *backpropagation*.

* Descenso por el gradiente requiere inicializar los pesos e iterar:

`\begin{equation}
w^{t+1} = w^t - \eta \nabla E(w^t)
\end{equation}`

* En cada iteración, accedemos a todos los datos para calcular `$\nabla E(w^t)\dots$`  complejidad `$\mathcal{O}(N)$`.

---

## Descenso por el gradiente estocástico (SGD)

* La función de coste tiene esta forma:

`\begin{equation*}
E(w) = \sum_{i=1}^N E_i(w)
\end{equation*}`

* En cada iteración, escogemos **un dato** al azar

`\begin{equation*}
w^{t+1} = w^t - \eta_t \nabla_w E_i(w^t)
\end{equation*}`

---

## Descenso por el gradiente estocástico (SGD)

* También podemos seleccionar un **minilote** `$\mathcal{B}$`

`\begin{equation*}
w^{t+1} = w^t - \eta_t \nabla_w \frac{1}{B} \sum_{i \in \mathcal{B}} f_i(w^t)
\end{equation*}`

* La complejidad pasa de `$\mathcal{O}(N)$` a `$\mathcal{O}(B)$`, además, no es necesario tener toda la matriz `$X$`, sino solo los datos del minilote `$\mathcal{B}$`.

* Otra ventaja: mayor probabilidad de escapar óptimos locales que con GD, un punto estacionario de la función objetivo en GD no lo será en SGD generalmente.

---

## Descenso por el gradiente estocástico (SGD)

* Usando resultados de aproximación estocástica de Robbins & Monro (1954), se puede demostrar convergencia a mínimo local siempre y cuando

1. Las tasas de aprendizaje cumplen estas condiciones:
`\begin{align*}
\sum_{t=0}^\infty \eta_t &= \infty \\
\sum_{t=0}^\infty \eta^2_t &< \infty
\end{align*}`

2. El gradiente que se utiliza en cada iteración es un estimador **no sesgado** del gradiente.

---

## Eecto de la estocasticidad

![:scale 100%](./img/sgd.png)

---

## Nuevos desarrollos

* **Momento (1986)**

Ayuda a amortiguar las oscilaciones que hacen que SGD sea lento.

`\begin{align*}
w^{t+1} &= w^t - v^{t+1} \\
v^{t+1} &= \gamma v^{t} + \eta_t \nabla_w E_i(w^t)
\end{align*}`

* **AdaGrad (2011)**

Adapta la tasa de aprendizaje a cada parámetro, disminuyéndola en parámetros con actualizaciones frecuentes (resp. aumentándola en parámetros con actualizaciones infrecuentes).

`\begin{equation*}
w^{t+1}_j = w^t_j - \frac{\eta}{\sqrt{G^t_{j,j} + \epsilon}} \nabla_w E_i(w^t)_j
\end{equation*}`

donde `$G^t_{j,j} = \sum_{t'=0}^t (\nabla_w f_i(w^t)_j)^2$` (la suma de los gradientes al cuadrado para esa coordenada hasta `$t$`)

---

## Nuevos desarrollos

* **RMSProp**

Adapta la tasa de aprendizaje dividiéndola por una media del cuadrado de los gradientes anteriores, que decae exponencialmente.

* **Adam**, evolución de AdaGrad.

* Muchos más...

* Una revisión de los diferentes optimizadores puede encontrarse en
[aqui](http://ruder.io/optimizing-gradient-descent/index.html#rmsprop).

---
class: middle, center, inverse
# Perceptrón muilticapa. Backpropagation

---
## Backpropagation (1)

* Técnica **eficiente** para evaluar `$\nabla E(w)$` aprovechando la estructura de perceptrones multicapa.

* En mayoría de problemas `$E(w) = \sum_n E_n (w)$`, nos centramos en evaluar `$\nabla E_n(w)$`.

* En un MLP, cada unidad calcula combinación lineal de sus inputs `$z_i$`, `$a_j = \sum_i w_{ji}z_i$`.

* Como output devuelve `$z_j = h(a_j)$`.

* Supongamos que para cada instancia the train, hemos calculado inputs y outputs de todas las neuronas (*forward propagation*).

* Evaluamos la derivada de `$E_n$` respecto `$w_{ji}$`

`\begin{equation}
\frac{\partial E_n}{\partial w_{ji}} = \frac{\partial E_n}{\partial a_j} \frac{\partial a_j}{\partial w_{ji}} := \delta_j z_i 
\end{equation}`

* Donde `$\delta_j = \frac{\partial E_n}{\partial a_j}$`.

---
## Backpropagation (2)

* Para calcular las derivadas, únicamente necesitamos calcular `$\delta_j$` para cada unidad.

* Para cualquier unidad oculta, `$E_n$` es función de `$a_j$`, únicamente a través de las `$a_k$` de la capa siguiente.

`\begin{equation}
\delta_j =  \frac{\partial E_n}{\partial a_j} = \sum_k \frac{\partial E_n}{\partial a_k} \frac{\partial a_k}{\partial a_{j}}
\end{equation}`

<center>
![:scale 50%](./img/back.png)
</center>

---
## Backpropagation (2)

* Efectuando las derivadas vemos que

`\begin{equation}
\delta_j =  h'(a_j) \sum_k w_{kj} \delta_k
\end{equation}`

* Para unidad de salida calcular `$\delta_j$` es trivial, e.g. `$E_n = \frac{1}{2} (y_n - t_n)^2$`, y la activación es la identidad, entonces

`\begin{equation}
\delta = y_n - t_n
\end{equation}`

---
## Backpropagation (3)

* El algoritmo

1. Meter vector `$x_n$` a la red y realizar el *forward pass* de la red, para calcular inputs y outputs en cada unidad.
  
  2. Evaluar `$\delta$` en la unidad de salida.
  
  3. Propagar las `$\delta$`'s hacia atrás para obtener `$\delta_j$` en cada unidad usando
`\begin{equation}
\delta_j =  h'(a_j) \sum_k w_{kj} \delta_k
\end{equation}`
  
  4. Evaluar las derivadas usando
`\begin{equation}
\frac{\partial E_n}{\partial w_{ji}} = \delta_j z_i 
\end{equation}`

---
## Backpropagation (4)

* Aspecto crucial de *backpropagation* es su eficiencia.

* Sea `$W$` el número totad de pesos.

* Calcular el gradiente usando *backpropagation*, requiere `$O(W)$` operaciones, para `$W$` suficientemente grande.

* Esto es así, pues el número de pesos suele ser mucho mayor que el número de neuronas.

* Esto implica que el cuello de botella en la computación es evaluar las combinaciones lineales. La evaluación de las activaciones requiere menos carga, pues hay tantas activaciones como neuronas.

---
## Backpropagation (5)

* **Ejercicio**: ¿Cuál es la complejidad de evaluar la derivada usando diferencias centrales?
`\begin{equation}
\frac{\partial E_n}{\partial w_{ji}} = \frac{E_n(w_{ji} + \epsilon) - E_n(w_{ji} - \epsilon)}{2 \epsilon} + O(\epsilon^2)
\end{equation}`

---
class: middle, center, inverse
# Perceptrón multicapa. Regularización

---

## Regularización (1)

* Número de unidades de input y output se eligen teniendo en cuenta la dimensionalida de los datos.

* Número de unidades ocultas `$M$`, es un hiperparámetro que regula la complejidad del modelo.

* Existirá un valor óptimo que equilibre entre underfitting y overfitting.

* Alternativa: escoger `$M$` lo suficientemente grande, y añadir regularizadores:

1. L2: `$\lambda\Vert w \Vert_2^2$`, conocido como *weight decay*.
  
  2. L1: `$\lambda \Vert w \Vert_1$`
  
---

## Regularización (2)

* Otra alternativa es usar *early stopping*.

* Como entrenamos de forma iterativa, podemos observar el comportamiento de una estimación del error de generalización mientras vamos entrenando.

* Guardamos un conjunto de validación, y en cada época, calculamos el error producido en este conjunto de validación.

* Observaremos que el error primero decrece, y después, cuando se hace overfitting, crece.

* Dejaremos de entrenar antes de que esto último suceda.

* Esto, en algunos casos, es equivalente a reducir la complejidad efectiva de la red.

---

## Regularización (3)

* Otra alternativa es usar *dropout*.

* En cada ejemplo de cada iteración del entrenamiento, "apagar" cada neurona con probabilidad `$1-p$`.

* En cada iteración se entrena una red de tamaño efectivo menor.

<center>
![:scale 90%](./img/dropout.png)
</center>

---
class: middle, center, inverse
# Redes Neuronales Bayesianas

---

## ¿Por qué BNNs?

* **Cuantifican la incertidumbre** en los pesos.

* **Cuantifican la incertidumbre** en la salida de la red.

* Permiten la selección directa de **hiperparámetros**, sin necesidad de validación.

* Previenen overfitting, y que la respuesta de la red es un "promedio" sobre muchas redes (cada una pesada con la distribución a posteriori).

`\begin{equation}
p(t \vert \mathcal{D}, x) = \int p(t \vert w, x) p(w \vert \mathcal{D}) dw
\end{equation}`

---

## ¿Por qué no BNNs?

* La dependencia **altamente no lineal** de la salida con los pesos, hace que la inferencia Bayesiana exact sea inviable.

* Métodos MCMC no escalan bien.

* Alternativas:

1. Versiones sofisticadas de MCMC, por ejemplo <a href="https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf">esto</a>. 
  
  2. Inferencia variacional: aproximar el posterior por una gaussiana multivariante (mean-field o full rank).

* Campo activo de investigación!